Norme sur un ev de dim finie

[legeniedesalpages]

Bonsoir,

j'ai un souci sur un point de mon cours de topo:

Soit un -espace vectoriel de dimension finie.

Théorème: Toutes les normes sur E sont équivalentes.

Corollaire: est compacte (indépendamment de la norme).

Je ne vois pas comment de ce théorème, on en déduit ce corollaire.

Merci pour votre aide.

[Dyo]

Hello,

Toutes les normes sur E sont équivalentes (en dimension finie). C'est déjà un corollaire de : Toutes les normes équivalentes sur .

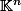
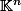
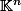
Cela entraîne que si E est de dimension finie, il existe un homéomorphisme de E dans . Or est localement compact donc E localement compact.

Et E localement compact implique que B(0,R) compact car homéomorphe à une boule de petit rayon B(0,r') (voisinage compact de 0). (On parle de boules fermées ici).

[legeniedesalpages]

Je vois, merci Dyo.