Norme et application lipschitizienne
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 08 Sep 2012, 13:55
par majin » 08 Sep 2012, 13:55
Bonjour,
On définit la norme qui de

dans
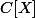
,
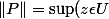\left | P(z) \right |)
avec

l'ensemble des complexes tel que leurs modules est égal à

.
Pour l'application qui à

de degré inférieur à

associe sa dérivé, j'avais montré qu'elle est lipschitzienne avec

la plus petite constante de Lipschitz.
Je voudrais montrer que l'application qui associe à

de C[X] sa dérivé n'est pas lipschitizienne mais je ne sais pas comment m'y prendre.
Merci de votre aide.
-
geegee
- Membre Rationnel
- Messages: 799
- Enregistré le: 11 Mai 2008, 13:17
-
 par geegee » 08 Sep 2012, 14:16
par geegee » 08 Sep 2012, 14:16
Bonjour,
En analyse mathématique, une application lipschitzienne (du nom de Rudolf Lipschitz) est une application possédant une certaine propriété de régularité qui est plus forte que la continuité. Intuitivement, c'est une fonction qui est limitée dans sa manière d'évoluer. Tout segment reliant deux points du graphe d'une telle fonction aura une pente inférieure à une constante appelée constante de Lipschitz.
http://fr.wikipedia.org/wiki/Application_lipschitzienne
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 08 Sep 2012, 14:18
par barbu23 » 08 Sep 2012, 14:18
Salut : :happy3:
Pour montrer qu'il n'est pas Lipschitzienne, tu trouves un exemple de

et

deux polynômes, tel que

:
 - f(Q) || > k || P - Q || $)
avec

...
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 08 Sep 2012, 14:43
par majin » 08 Sep 2012, 14:43
barbu23 a écrit:Salut : :happy3:
Pour montrer qu'il n'est pas Lipschitzienne, tu trouves un exemple de

et

deux polynômes, tel que

:
 - f(Q) || > k || P - Q || $)
avec

...
J'avais pensé au polynôme
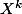
mais la constante de Lipschitz dépend du polynôme, donc est-ce que c'est le bon exemple?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 08 Sep 2012, 14:47
par barbu23 » 08 Sep 2012, 14:47
majin a écrit:Oui justement c'est ce j'avais essayé de faire, mais j'ai rien trouvé.
Moi, j'ai peut être déjà fait cette exercice avant, mais, je ne me souviens pas des détails.
Tu considère, je pense
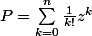
et

... :hein:
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 08 Sep 2012, 14:49
par majin » 08 Sep 2012, 14:49
barbu23 a écrit:Moi, j'ai peut être déjà fait cette exercice avant, mais, je ne me souviens pas des détails.
Tu considère, je pense
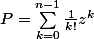
et

... :hein:
Mais la constante dépend du polynôme, c'est pas un problème?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 08 Sep 2012, 14:54
par barbu23 » 08 Sep 2012, 14:54
majin a écrit:Mais la constante dépend du polynôme, c'est pas un problème?
Tu remplaces l'indice

, par

, pour éviter les confusions.
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 08 Sep 2012, 16:45
par Maxmau » 08 Sep 2012, 16:45
majin a écrit:Bonjour,
Pour l'application qui à

de degré inférieur à

associe sa dérivé, j'avais montré qu'elle est lipschitzienne avec

la plus petite constante de Lipschitz.
Merci de votre aide.
Bonjour
Si f est k- lipchitzienne sur C[X] , elle est k-lipchitzienne sur Cn[X]
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 08 Sep 2012, 17:44
par majin » 08 Sep 2012, 17:44
Maxmau a écrit:Bonjour
Si f est k- lipchitzienne sur C[X] , elle est k-lipchitzienne sur Cn[X]
Oui, mais dans mon exo, f est k-lipschtizienne sur C[X] et je doit montrer qu'elle ne l'est pas sur C[X]
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 08 Sep 2012, 18:01
par majin » 08 Sep 2012, 18:01
barbu23 a écrit:Tu remplaces l'indice

, par

, pour éviter les confusions.
Je ne pense pas que la méthode serait de trouver un polynome P et Q qui ne vérifient pas l'inégalité pour n'importe quel k, parce que il suffit de prendre k=deg(P-Q) et on aura l'inégalité vrai.
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 09 Sep 2012, 10:06
par Maxmau » 09 Sep 2012, 10:06
majin a écrit:Oui, mais dans mon exo, f est k-lipschtizienne sur C[X] et je doit montrer qu'elle ne l'est pas sur C[X]
Par absurde
Si f est k- lipchitzienne sur C[X] , elle est k-lipchitzienne sur Cn[X]
Donc (d'après ce qui précède) k >= n cela quel que soit n . Conclusion?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités