Bonjour,
Pourriez-vous m'aider dans l'exercice suivant, je suis bloqué au début de la question 2.
Soit
et
deux entiers positifs,
désigne l'ensemble des entiers strictement positifs inférieurs ou égaux à
.
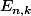
désigne l'ensemble des partitions strictes de
en
sous-ensembles. Les
sont dans
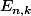
si et seulement si les
sont des sous-ensembles non vides deux à deux disjoints de
tel que l'union des
soit
.
désigne l'union des
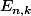
pour
variant de
à
. On note
le cardinal de
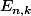
et
celui de
. Les
sont les nombres de Stirling. Les
sont les nombres de Bell.
1)
a) Donner les valeurs de
et
pour n=1,2,3
b) Vérifier que
. Que peut-on dire de
pour
strictement supérieur à
c) Calculer
et
d) Justifier la relation:
2)
On considère la partition de
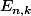
en deux sous-ensemble:
,
a) Établir une bijection entre
et
b)Etablir une surjection de
![](https://latex.ilemaths.net/ile_TEX.cgi?E_{n,k}^{"})
et
. Déterminer le nombre d'antécédents d'un élément de
c) En déduire que pour tout
entier naturel non nul et pour tout
entier naturel au moins égal à 2:
Je vous remercie d'avance
