Formule de Stirling
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Memento
- Membre Naturel
- Messages: 71
- Enregistré le: 13 Jan 2008, 18:17
-
par Memento » 17 Jan 2008, 21:04
Bonsoir à tous,
Voici mon problème je cherche a retrouver la formule de Stirling:
 sqrt(2.Pi.n))
quand
par une methode "perso": voici comment j'ai tenté de le faire :
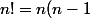 (n-2) ... 1)
ce qui peut s'écrire:
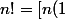] [n (1-1/n)] [n (1-2/n)] ... [n (1-(n-1)/n)])
(n termes entre crochets)
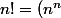 (1) (1-1/n) (1-2/n) ... (1-(n-1)/n))
posons :
=(1) (1-1/n) (1-2/n) ... (1-(n-1)/n))
(n termes)
=[1-0 (1/n)] [1-1 (1/n)] [1-2 (1/n)] ... [1-(n-1) (1/n)])
Comme:
=exp(ln(p1(n))))
On peut écrire:
=exp(ln([1-0 (1/n))] [1-1 (1/n)] [1-2 (1/n)] ... [1-(n-1) (1/n)])))
Posons:
=ln([1-0 (1/n)] [1-1 (1/n)] [1-2 (1/n)] ... [1-(n-1) (1/n)]))
=ln(1-0 (1/n)) + ln(1-1 (1/n)) + ln(1-2 (1/n)) + ... + ln(1-(n-1) (1/n)))
comme :
= n (1/n) p2(n))
on a:
= n (1/n) (ln(1-0(1/n)) + ln(1-1(1/n)) + ln(1-2(1/n)) + ... + ln(1-(n-1)(1/n))))
Or,
Nous savons pour tout
compris entre
et
,
:
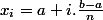
Alors la somme:
\,)
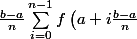tend vers
 dt\,)
lorsque
tend vers
.
en posant alors dans p2(n):
=(1/n) (ln(1-0(1/n)) + ln(1-1(1/n)) + ln(1-2(1/n)) + ... + ln(1-(n-1)(1/n))))
on reconnait une formule de calcul d'integral comme vu precedemment:
en effet:
si
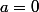
et
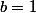
On a:
=\frac{b-a}{n}\sum_{i=0}^{n-1}f\left(a+i\frac{b-a}{n}\right)\,)
avec :
=ln(1-x))
quand n tend vers l'infini :
)
tend donc vers
 dt\,)
D'ou:
 = -(0.ln(0)-0+1))
Donc:
 = -1)
D'ou:
Comme
 = n I(n))
 \sim -n)
quand
et comme
=exp(p2(n)))
 \sim exp(-n))
quand
et
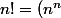 p1(n))
exp(-n))
quand
au lieu de
 sqrt(2.Pi.n))
quand
Je ne comprends pas ou se situe mon erreur, merci de m'aiderMemento
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
par Lierre Aeripz » 17 Jan 2008, 23:24
Je n'ai pas tout lu en détails, mais j'ai trouvé quelques fautes.
Admettons que ton intégrale tende vers -1.
On a donc
\sim_{n\to\infty} -n)
Et pas
\to_{n\to\infty} -n)
qui n'a aucun sens si on ne précise rien.
Or les équivalents ne se composent pas... Et surtout pas par l'exponentielle. Pour t'en convaincre, refait la fin de tes calculs en supposant que ton intégrale (que j'appelle
) vaut
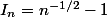
, qui tend bien vers -1.
-
Memento
- Membre Naturel
- Messages: 71
- Enregistré le: 13 Jan 2008, 18:17
-
par Memento » 17 Jan 2008, 23:45
Oui très juste,
Mais est-ce que cela remet en cause mon résultat finale,
car j'ai refait le calcul de mon intégrale et j'ai bien:
 = -1)
donc
quand
Je ne vois pas d'ou viens mon erreur
@+
-
Memento
- Membre Naturel
- Messages: 71
- Enregistré le: 13 Jan 2008, 18:17
-
par Memento » 18 Jan 2008, 17:08
J'ai mis au propre mon message ! :happy:
Personne pour m'aider ???
Merci !
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
par Joker62 » 18 Jan 2008, 17:20
Bon j'ai pas vérifier parce que c'est affreux, mais j'te conseille de regarder de ce côté :
tu dis p2(n) ~ -n => p1(n) ~ e(-n)
Donc en gros tu dis :
f ~ g => e^f ~ e^g
Or ceci n'est pas toujours vrai !
C'est vrai si et seulement si f-g tend vers 0
Donc calcule la limite de p2(n) + n
Si c'est pas 0, le problème est là, sinon je sais pas :)
Ah zut ! j'avais même pas lu le premier message !
Désolé :(
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 18 Jan 2008, 17:27
Memento a écrit:Nous savons pour tout
compris entre
et
,
:
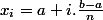
Alors la somme:
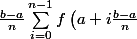tend vers
lorsque
tend vers
.
quand
et comme
1- Achtung quand même aux sommes de Riemann associées aux intégrales pas propres. Ici ça marche parceque ln(1-x) est monotone mais, à mon avis (qui vaut pas grand chose ici), il faut mieux le dire.
2- (si j'ai bien compris ce que tu fis) c'est pas parce que u(n) ~ v(n) que exp(u(n)) ~ exp(v(n)) (contrex : n²+n ~ n²)
-
Memento
- Membre Naturel
- Messages: 71
- Enregistré le: 13 Jan 2008, 18:17
-
par Memento » 18 Jan 2008, 18:49
Merci Jocker,
(affreux) au moins m'a méthode a l'avantage de soulever un problème intéressant, et si tu avais pu la lire en détail tu l'aurais trouvé assez originale:
Ceci dit vous avez certainement raison, le problème doit venir de,
) \sim exp(-n))
pour
Lim
+n)
quand
J'ai essayé:
+n > p2(n)+ln(n))
quelque soit
positif
Or:
+ln(n)=ln([1-0 (1/n)] [1-1 (1/n)] [1-2 (1/n)] ... [1-(n-1) (1/n)]) + ln(n))
+ln(n)=ln(n [1-0 (1/n)] [1-1 (1/n)] [1-2 (1/n)] ... [1-(n-1) (1/n)]))
+ln(n)=ln(n (n-1) (n-2) ... 1))
+ln(n)=ln(n!))
quand n tend vers l'infini :
+ln(n)-> +\infty)
D'ou comme
+n>p2(n)+ln(n))
pour tout n positif
Donc :
+n -> +\infty)
Donc l'erreur se situerai bien la...
@+
-
Thalès
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Fév 2007, 19:51
-
par Thalès » 18 Jan 2008, 19:20
Je pense qu'il serait plus facile de retrouver la formule de Stirling en utilisant la fonction ;) d'Euler.
-
Memento
- Membre Naturel
- Messages: 71
- Enregistré le: 13 Jan 2008, 18:17
-
par Memento » 18 Jan 2008, 20:05
Oui Thales,
Avec la fonction gamma c'est la méthode habituelle,
en fait ma méthode est une simple curiosité dont j'ai voulu tester la validité..
Merci à toi !
@+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
