Démo de la formule de stirling à l'aide de l'intégrale de wa
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 06 Nov 2010, 16:49
par mimix » 06 Nov 2010, 16:49
bonjour,
j'essaye de redémontrer la formule de stirling avec l'intégrale de wallis, et je bloque à la fin:
dans la démo du cours, j'ai:
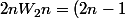 W_{2n-2}.)
D'où:
W0}{2.4...2n}.)
Je ne vois pas le passage entre les 2 étapes. Y a forcément une histoire de factorielles, mais je bloque!
Je rappelle l'intégrale de Wallis:
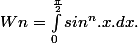
Merci
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 06 Nov 2010, 16:58
par benekire2 » 06 Nov 2010, 16:58
Salut, le passage entre tes deux étapes, c'est un récurrnence.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Nov 2010, 17:01
par Ben314 » 06 Nov 2010, 17:01
Salut,
Comme,
pour tout entier n,
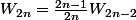
, tu as :
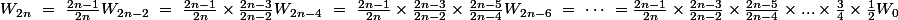
.
Bien sûr, si tu n'aime pas les points de suspension, ben la preuve "archi rigoureuse" c'est clairement une récurrence.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 06 Nov 2010, 17:05
par mimix » 06 Nov 2010, 17:05
je sais pas quoi faire, quand j'obtiens: W2n = [ (2n-1)/2n ]. W2n-2
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 06 Nov 2010, 17:07
par benekire2 » 06 Nov 2010, 17:07
Cela dit on comprends toujours bien par les pointillés :we:
Puis si tu tient à ta factorielle et que t'aime pas les points de suspension dans un résultat , tu écris
!}{2^{2n}(n!)^2}W_0=\frac{\pi(2n)! }{2^{2n+1}(n!)^2})
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 06 Nov 2010, 17:09
par mimix » 06 Nov 2010, 17:09
merci ^^ :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
