Nombre de relations Antisymétriques

[irrationnel]

Bonjour,

Je me posé la question suivante :
combien de relations antisymétriques existe t-il sur un ensemble de cardinal n ?

Je sais que pour les relations Réflexives c'est 2^n(n-1)
et pour les relations Symétriques 2^(n(n+1))/2.
De plus la définition d'une relation antisymétrique est défini par :
x R y et y R x => y = x quelque soit y,x dans E où E est un ensemble.

Merci

[zygomatique]

salut

comment trouves-tu le nombre de relations réflexives ?

donc pour chaque couple (x, y) avec x <> y tu as deux cas qui s'excluent : soit x R y soit y R x

[irrationnel]

Salut
Pour le nombre de relation réflexives j'ai trouvé l'explication sur ce site :
[url]: http://nte-serveur.univ-lyon1.fr/immedi ... e_7_7.html[/url]

Je n'ai pas vraiment tout compris mais sur ce même site il indique aussi qu'il y a 2^n relation symétrique et antisymétrique à la fois dans je pense que le nombre de relation antisymétrique est de 2^n - 2^(n(n+1))/2 .
Je comprend pas comment on peut trouver TOUTES les relation réflexives,symétriques ou antisymétrique sur un ensemble donné

[chombier]

Tu peux représenter une relation sur un ensemble E à n éléments par une matrice de taille (n,n) à valeurs dans {0 ; 1}. Il y a donc 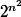relations binaires sur E

Parmi toutes ces matrices, lesquelles représentent des relations symétriques ? Et combien y en a-t-elle ?

Si n=3, et que je te donne la matrice et que je te dis qu'elle représente une relation symétrique, peux-tu compléter la matrice ?

[irrationnel]

Salut,

Je dirais que les matrices représentant une relation symétrique sont celles qui vérifient la condition
non(xRy) ou yRx, et c'est la que je bloque puisque je vois pas comment les énumérer .

Pour la matrice je dirais : ?

[zygomatique]

on ne peut pas les trouver toutes enfin on peut les lister toutes ... mais ça n'a aucun intérêt ...

le lien que tu donnes ne fait que les compter ...

effectivement il est plus difficile de compter les relations antisymétriques ...

tuas trois cas pour x <> y

x R y = y Rx = 0
x R y = 1 et y R x = 0
x R y = 0 et y R x = 1

[irrationnel]

Je commence à voir un plus clair, j'ai compris pour les relations réflexives et symétriques.

Pour les relations antisymétriques , ils doivent vérifier : .

j'étudie ton message zygomatique pour essayer de comprendre

[irrationnel]

Merci Ben314 !

[Ben314]

Non, j'ai écrit une connerie (et je l'ai effacé...)
Pour les relation antisymétriques, comme le dit zygo., c'est effectivement pas la même chose.
Le raisonnement qu'il faut tenir, c'est de dire que :
- Sur la diagonale (n termes), on prend n'importe quoi => 2^n possibilité.
- Les autres (=n²-n=n(n-1)) termes on les regroupe par deux : la case (x,y) et la case (y,x) (donc ce qui fait n(n-1)/2 couples) et pour chacune de ces couple de cases, on peut mettre (0,0) ou (1,0) ou (0,1) mais pas (1,1) donc 3 possibilités => 3^(n(n-1)/2) possibilités.