Salut, je me permets de compléter la réponse de LB2 en reprenant point par point les interrogations.
mehdi-128 a écrit:Supposons que n ne soit pas un carré parfait, alors

. Cet entier n admet donc au moins un diviseur premier p avec une puissance impaire.
 Pourquoi une puissance impaire forcément ? Ca veut dire quoi un nombre premier avec une puissance impaire ?
Pourquoi une puissance impaire forcément ? Ca veut dire quoi un nombre premier avec une puissance impaire ?
Ça veut dire que dans la décomposition de

en produit de facteurs premiers, (
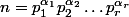
)le diviseur premier

apparaît d'une part (car p divise n), c'est à dire que c'est l'un des

et sa puissance
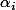
est impaire.
Ensuite, tu poses la question de pourquoi ?
En fait, si tu prends un entier n de décomposition en facteurs premiers
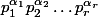
, alors il est très facile de comprendre que :

est un carré parfait si et seulement si tous les
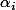
sont pairs. (**)
Admettant ceci un instant, il est donc clair que si n n'est pas un carré parfait,alors c'est que l'un au moins de ses diviseurs premiers apparaît avec une puissance impaire.
Démo de (**)
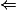
:
Si tous les
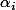
sont pairs, ils s'écrivent

et donc, on a :
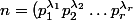^2)

:
Si n = m^2, en écrivant la décomposition en facteurs premiers de m:
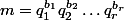
, on a alors :
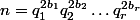
Par unicité d'une telle décomposition, on voit bien que les puissances apparaissant dans la décomposition de n sont paires.
Ensuite, raisonnons par l'absurde et supposons que
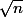
est rationnel. Il existerait alors des entiers naturels a et b non nuls tels que
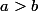
et :
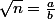
 Pourquoi nécessairement a>b ?
Pourquoi nécessairement a>b ?
Comme
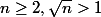
et donc
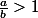
donc
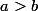
Et là je comprends plus rien ci-dessous :
On constate que le nombre premier p apparait avec une puissance impaire pour
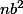
et avec une puissance paire pour

 Comment on peut savoir à quel puissance apparaît le nombre premier p ? Pourquoi c'est impair pour
Comment on peut savoir à quel puissance apparaît le nombre premier p ? Pourquoi c'est impair pour 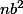 dt pair pour
dt pair pour  ?
? Merci d'avance.
LB2 a écrit:Bonsoir mehdi-128,
pour comprendre à quelle puissance apparaît p, on écrit la décomposition en facteurs premiers.
Par hypothèse p apparaît avec une puissance impaire dans n (cf point 1. , sinon n serait un carré parfait)
Mais p apparaît avec une puissance paire dans b^2, puisque b^2 est un carré.
Donc p apparaît avec une puissance impaire dans nb^2 (impair + pair = impair)
Même raisonnement pour a^2.
A bientôt
Pseudo modifié : anciennement Trident2.

