Nombre complexe

[dizzee]

bonjours a vous tous je suis nouveau sur le forum.Je suis etudiant en 1er année D'IUT GEII,venant dune terminale s. Je sais resoudre des equation complexe du second ou quatrieme degres avec un discriminant réel. M ais hier jai eu a resoudre des equation complexe avec un discriminant imaginaire ex 32i. Jaimerais savoir quelle methode a dopter sachant que celle de mon professeur me parais peu clair. merci a vous tous. je vous laisse un exemple dune equation que jai u a resoudre :z²-2(3-2i)+5-20i=0

z^4-(5-14i)z²-2(12+5i)=0

ps: je ne vous demande pas de les resoudre juste de m'expliquer la methode a adopter. cdt.

[nuage]

Salut,
quand le discriminant est complexe, on fait comme quand il est réel :
on cherche un nombre tel que 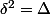et les solutions sont
étant une racine carrée de

Le problème est d'exprimer ce nombre avec des radicaux réels.

C'est assez facile pour 32i car


Pour la deuxième équation que tu proposes je n'ai pas l'impression que ce soit possible.

[AlexisD]

Pour la deuxième il faut d'abord poser Z=z² puis résoudre ton équation avec la variable Z.
Une fois les solutions Z1 et Z2 trouvées, il faut résoudre:
z²=Z1; z²=Z2

[dizzee]

le probleme c'est que mon discriminant est imaginaire comme jécris les solution si je connais pas le signe du discriminant?

[nuage]

Quand on résout une équation du 2° degré dans il n' y a que deux cas :
le discriminant est nul, il y a une racine double
le discriminant n'est pas nul, il y a deux racines distinctes.

[Black Jack]

Pour la 2ème équation (après avoir posé Z = z²)

Le discriminant est complexe (pas imaginaire)

Il faut donc trouver les racines carrées d'un nombre complexe:

De manière générale :

(zd)² = a + ib

|zd²| = V(a²+b²)

arg(zd) = ...
Si a > 0, arg(zd) = arctg(b/a + 2k.Pi)
Si a < 0, arg(zd) = Pi + arctg(b/a + 2k.Pi)

Donc |zd| = (a²+b²)^(1/4)
et:
si a > 0, arg(zd) = (1/2).arctg(b/a + k.Pi)
Si a < 0, arg(zd) = Pi/2 + (1/2).arctg(b/a + k.Pi)

--> zd = +/- (a²+b²)^(1/4) * (cos(Phi) + i.sin(Phi))
Avec:
Phi = (1/2).arctg(b/a) si a > 0
et
Phi = Pi/2 + (1/2).arctg(b/a) si a < 0

:zen:

[mathelot]

bonjour,

je continue les explications de Nuage , pour la (2):

effectivement on calcule
il faut en trouver une racine carrée complexe .

L'équation d'une telle racine est


les deux premières égalités donnent des valeurs possibles pour x et y.
la troisième indique que le signe du produit xy doit être celui de

une fois les racines en écrites, on recommence
car l'équation est bicarrée