Nombre complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Andamir93
- Membre Naturel
- Messages: 62
- Enregistré le: 22 Mar 2020, 15:18
-
 par Andamir93 » 19 Avr 2020, 17:11
par Andamir93 » 19 Avr 2020, 17:11
Bonjour,
Pourriez-vous m'aider dans mes différents exercice de math ? Je ne comprend pas le cours donner par le professeurs donc si vous auriez également un cours permettant une compréhension meilleur je suis preneur:

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 19 Avr 2020, 19:28
par Carpate » 19 Avr 2020, 19:28
Bonsoir
Qu'as-tu fait ?
L'exercice 1 est élémentaire.
La partie réelle de z est constante : 2 et la partie imaginaire décrit R
Quelle peut bien être cette droite ?
Je doute qu'un autre cours te soit utile
0rthographe fantaisiste !
-
Andamir93
- Membre Naturel
- Messages: 62
- Enregistré le: 22 Mar 2020, 15:18
-
 par Andamir93 » 20 Avr 2020, 06:59
par Andamir93 » 20 Avr 2020, 06:59
Bonjour,
Pour ce qui concerne l’exercice 1, voici ce que j'ai trouver pour la première question :
https://zupimages.net/viewer.php?id=20/17/b52m.png mais comment donner un ensemble ? J'ai envie de dire que l'ensemble des points M est compris entre ]-00;0]U[0;+00[ est ce bon ?
-
Andamir93
- Membre Naturel
- Messages: 62
- Enregistré le: 22 Mar 2020, 15:18
-
 par Andamir93 » 20 Avr 2020, 07:01
par Andamir93 » 20 Avr 2020, 07:01
Ensuite pour la partie deux de l'exercice 1, je ne sais pas comment représenter Im(z-1)=3. J'ai pour idée de refaire le même schéma avec une droite horizontal dans l'axe des ordonnées au cordonnée (0;3) mais encore une fois est-ce bon ma démarche ? Merci bien !
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 20 Avr 2020, 08:42
par Carpate » 20 Avr 2020, 08:42
Oui, on voit tout de suite que le lieu est la perpendiculaire en (3; 0) à l'axe des abscisses soit la droite d'équation cartésienne x = 3
Pour le démontrer :
Soit
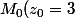)
et
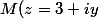)
L'affixe de
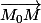
est
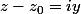
 = arg(iy) =arg(i) +arg(y) =\frac{\pi}{2} +arg(y))
(modulo
)
Si
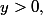
 = 0)
et
 = \frac{\pi}{2})
M décrit la demi-droite perpendiculaire en
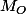
à l'axe des abscisses et orientée "vers le haut".
Si
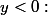
 =\pi)
et
 = \frac{3\pi}{2})
M décrit la demi-droite perpendiculaire en
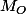
à l'axe des abscisses et orientée "vers le bas".
L'ensemble est donc la droite perpendiculaire en

à l'axe des abscisses.
-
Andamir93
- Membre Naturel
- Messages: 62
- Enregistré le: 22 Mar 2020, 15:18
-
 par Andamir93 » 20 Avr 2020, 08:46
par Andamir93 » 20 Avr 2020, 08:46
D'accord, merci bien. Pourriez-vous me donner des indications pour la question 2 de l'exercice 1 ? Afin que je puisse également essayer de trouver la réponse et comprendre par la même occasion
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 20 Avr 2020, 09:03
par Carpate » 20 Avr 2020, 09:03
je ne sais pas comment représenter Im(z-1)=3
C'est plutôt Im(z-
i) = 3
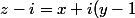)
Im(z-i) = 3
y-1=3
y=4
droite d'équation y = 4
Modifié en dernier par
Carpate le 20 Avr 2020, 09:05, modifié 1 fois.
-
Black Jack
 par Black Jack » 20 Avr 2020, 09:04
par Black Jack » 20 Avr 2020, 09:04
Andamir93 a écrit:Ensuite pour la partie deux de l'exercice 1, je ne sais pas comment représenter Im(z-1)=3. J'ai pour idée de refaire le même schéma avec une droite horizontal dans l'axe des ordonnées au cordonnée (0;3) mais encore une fois est-ce bon ma démarche ? Merci bien !
Ex1
2)
Im(z-i) = 3
z = a + ib
z-i = a + i(b-1)
Im(z-i) = b-1
--> b-1 = 3
b = 4
z = a + 4i (avec a un réel quelconque)
Le lieu des points M est la droite d'équation y = 4 dans le plan complexe (soit une parallèle à l'axe des réels passant par le point P(0 ; 4))


-
vam
- Admin
- Messages: 681
- Enregistré le: 09 Aoû 2019, 09:50
-
 par vam » 20 Avr 2020, 09:07
par vam » 20 Avr 2020, 09:07
Pour mettre une image, vous pouvez aller sur
https://postimages.org/fr/Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

-
Andamir93
- Membre Naturel
- Messages: 62
- Enregistré le: 22 Mar 2020, 15:18
-
 par Andamir93 » 20 Avr 2020, 09:10
par Andamir93 » 20 Avr 2020, 09:10
Je ne fais que poser mes questions sur d'autre site rien ne m'en empêche je cherche à comprendre les mathématiques ^^

-
vam
- Admin
- Messages: 681
- Enregistré le: 09 Aoû 2019, 09:50
-
 par vam » 20 Avr 2020, 09:14
par vam » 20 Avr 2020, 09:14
non, mais connecté des deux côtés simultanément pour poser les mêmes questions, faut pas abuser...
Pour mettre une image, vous pouvez aller sur
https://postimages.org/fr/Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

-
Andamir93
- Membre Naturel
- Messages: 62
- Enregistré le: 22 Mar 2020, 15:18
-
 par Andamir93 » 20 Avr 2020, 09:17
par Andamir93 » 20 Avr 2020, 09:17
Je reçois des réponses sur les deux sites donc je répond sur les deux sites. Sa me permet de voir plusieurs méthode. Rien ne m’empêche de faire cela, si ? Est-je manqué au règlement du forum ?
-
Andamir93
- Membre Naturel
- Messages: 62
- Enregistré le: 22 Mar 2020, 15:18
-
 par Andamir93 » 20 Avr 2020, 09:24
par Andamir93 » 20 Avr 2020, 09:24
Black Jack a écrit: Andamir93 a écrit:Ensuite pour la partie deux de l'exercice 1, je ne sais pas comment représenter Im(z-1)=3. J'ai pour idée de refaire le même schéma avec une droite horizontal dans l'axe des ordonnées au cordonnée (0;3) mais encore une fois est-ce bon ma démarche ? Merci bien !
Ex1
2)
Im(z-i) = 3
z = a + ib
z-i = a + i(b-1)
Im(z-i) = b-1
--> b-1 = 3
b = 4
z = a + 4i (avec a un réel quelconque)
Le lieu des points M est la droite d'équation y = 4 dans le plan complexe (soit une parallèle à l'axe des réels passant par le point P(0 ; 4))

Merci pour l'aide

-
Andamir93
- Membre Naturel
- Messages: 62
- Enregistré le: 22 Mar 2020, 15:18
-
 par Andamir93 » 20 Avr 2020, 09:24
par Andamir93 » 20 Avr 2020, 09:24
Carpate a écrit: je ne sais pas comment représenter Im(z-1)=3
C'est plutôt Im(z-
i) = 3
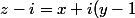)
Im(z-i) = 3
y-1=3
y=4
droite d'équation y = 4
Merci pour l'aide

-
Andamir93
- Membre Naturel
- Messages: 62
- Enregistré le: 22 Mar 2020, 15:18
-
 par Andamir93 » 20 Avr 2020, 09:25
par Andamir93 » 20 Avr 2020, 09:25
Pour l'exercice deux, voici ce que j'ai commencer à faire :
Déterminer et représenter l’ensemble des M d’affixe z telle que |z - 1-2i| = 3.
A(2i)
M(z)
En appliquant la formule du module : AB=|zB-zA |
AM=3
L’ensemble définit par cette égalité, est le cercle de centre A(2i) et de rayon 3
Est-ce correct ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 20 Avr 2020, 10:55
par Carpate » 20 Avr 2020, 10:55
j'ai commence
r à faire :
commencé : décidément tu as des problèmes avec la conjugaison des verbes
L’ensemble définit par cette égalité, est le cercle de centre A(2i) et de rayon 3
Ce cercle correspond à |z-2i| = 3 et non à
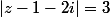
|z -1 -2i| = |z -(1+2i)|
Soient A(1+2i), M(z)
Que représente |z -(1+2i)| ?
-
Andamir93
- Membre Naturel
- Messages: 62
- Enregistré le: 22 Mar 2020, 15:18
-
 par Andamir93 » 20 Avr 2020, 11:58
par Andamir93 » 20 Avr 2020, 11:58
Je ne connais pas la réponse à cette question. Pourriez-vous me donner plus d'indice ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 20 Avr 2020, 12:15
par Carpate » 20 Avr 2020, 12:15
C'est pas sorcier.
Le vecteur AM a pour affixe z-(1+2i)
Donc lz-(1+2il est... de AM
-
Andamir93
- Membre Naturel
- Messages: 62
- Enregistré le: 22 Mar 2020, 15:18
-
 par Andamir93 » 20 Avr 2020, 12:21
par Andamir93 » 20 Avr 2020, 12:21
Je n'arrive pas à comprendre ce que vous avez écrit après le "donc"
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 20 Avr 2020, 13:46
par Carpate » 20 Avr 2020, 13:46
Je ne comprends pas, tu avais écrit :
A(2i)
M(z)
En appliquant la formule du module : AB=|zB-zA |
AM=3
L’ensemble définit par cette égalité, est le cercle de centre A(2i) et de rayon 3
Et là, pour
)
, tu ne vois pas ce que signifie
|)
, module de l'affixe de
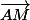
A (1+2i )
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités

