Nombre complexe

[Andamir93]

J'ai regarder une vidéo qui montrait comment faire ce genre de question et j'ai essayer de reproduire la méthode. Du coup si je comprend bien la réponse est : L’ensemble définit par cette égalité, est le cercle de centre A(1-2i) et de rayon 3

[Carpate]

Oui !
A part qu'il s'agit de A (1+2i)
Résumons :
On cherche l'ensemble des points M d'affixe vérifiant .

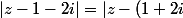donc si a pour affixe 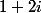, est l'affixe de et

Et si tu passais à la question 3 ...

[Andamir93]

Je suis justement entrain de faire la question 3 actuellement mais pour ce qui concerne la question 2 :

Déterminer et représenter l’ensemble des M d’affixe z telle que arg(z− 2−i) = pi/3

Je n'est rien trouver me permettant de comprendre comment répondre a ce genre de question. Auriez-vous une idée ?

[Carpate]

Je voulais dire question 2.
Même démarche : cherche de quel vecteur est l'affixe (sachant que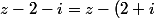
Ensuite utilise la signification géométrique de l'argument d'un nombre complexe (cours).

[Andamir93]

Très bien, j'essaie cela et je vous transmets ma réponse merci pour l'aide ! Je commence à comprendre !

[Carpate]

Alors , la réponse est ...

[Andamir93]

Alors désolé, hier j'ai eu un contre temps qui m'a empêcher de continuer l'exercice. Donc j'aurai dit que A a pour affixe 2+i donc que z-(2+i) est l'affixe de AM

[Andamir93]

Pour la définition d'un argument j'ai sa : mais je ne vois pas comment cela peut m'aider

[Carpate]

Rappel de la question :
Ensembles de points d'affixe tels que



Donc en utilisant le définition que tu as trouvée :

modulo
étant le vecteur unitaire de l'axe

Edit : Pour se ramener à la définition de l'argument d'un vecteur d'origine O il suffit de tracer le vecteur passant par O et équipollent à V, il a même argument que V.

[Andamir93]

Après la phrase du vecteur unitaire je n'est pas compris. Pourriez-vous répliquer ? Je dois tracer un vecteur d'origine 0 et d'angle pi/3 ?

[Andamir93]

et je crois qu'on a pas de vecteur V ?

[Carpate]

est l'angle que fait avec
L'ensemble recherché est donc la droite passant par et faisant un angle de avec

[Andamir93]

D'accord, mais on doit pas avoir un vecteur ? C'est à dire quelle est la longueur de AM ?

[Carpate]

On se fout de la longueur de 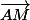. Il y en a une infinité.
Le point décrit la droite passant par et faisant un angle de 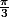avec

[Andamir93]

D'accord donc je fait juste un vecteur avec un angle de pi/3 ? Et je dit que l'ensemble des points m est représenter dessus ?

[Carpate]

Oui, tu traces la droite en question st tu y places un point M pour visualiser un vecteur AM dont l'argument est

Edit : Je m'aperçois que la "droite en question" est en fait la demi-droite d'origine A située dans le demi-plan supérieur (au-dessus de A).
L'autre demi-droite correspondrait à un angle de

[Andamir93]

je n'est pas compris "l'édit" pourrait tu me montrer sur un schéma ?

[Carpate]

Andamir93, là tu exagères !
C'est toi qui va dessiner un vecteur AM tel que et tu te rendras compte que le point M ne peut que se situer que sur la demi-droite " allant vers le haut" et que l'autre demi-droite (donc à l'opposé) correspond à
J'ai l'impression que tu ne fais pas beaucoup d'effort de compréhension.

[Andamir93]

Ahhhhhhhhh si j'ai compris ce que tu veux dire, c'est le demi plan supérieur que je n'avais pas compris désolé. Merci !

[Carpate]

J'espère que la question 2-3), classique, ne t'a pas posé de problème ...
Au fait pour quoi un Exercice 3 identique à l'Exercice 4 ?