Le mieux est de prendre un exemple numérique : n=5, p=3. Le nombre d'applications injectives est
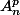
=5*4*3=60 (nombre de façons de choisir
dans l'ordre 3 éléments parmi 5). Parmi ces applications, certaines ont le même ensemble image, par exemple f(1)=5, f(2)=1, f(3)=4, et g(1)=1, g(2)=4, g(3)=5, ont le même ensemble image {1,4,5}. Il y a 3!=6 applications qui ont le même ensemble image (6=nombre de façons d'ordonner 1,4,5). Parmi ces 6 applications, une seule est strictement croissante (c'est la 2ème de mon exemple).
Reprenons. Pour chaque ensemble image, il y a 3! applications injectives dont 1 seule strictement croissante. Donc, pour obtenir le nombre d'applications strictement croissantes, on divise le nombre d'applications injectives : 60, par le nombre d'ensembles images : 3!, cela en fait 10 =
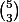
.
On peut dire aussi directement qu'il y a
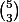
ensembles images (nombre de façons de choisir 3 éléments parmi 5, l'ordre ne comptant pas) et 1 seule application strictement croissante par ensemble image, donc il y a en 10.
