Nilpotence matrice triangulaire supèrieur diagonale nulle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 27 Juin 2017, 22:27
par infernaleur » 27 Juin 2017, 22:27
Salut !
Je m’intéressais à démontrer la nilpotence d'une matrice triangulaire supérieur à diagonale nulle mais je n'y parviens pas ...
Auriez-vous quelques pistes à me donner

Merci !!!
-
Viko
- Membre Relatif
- Messages: 209
- Enregistré le: 18 Juin 2017, 23:51
-
 par Viko » 27 Juin 2017, 22:31
par Viko » 27 Juin 2017, 22:31
la seule démonstration que je connaisse le démontre en considérant que les matrices sont des représentations matricielles d'endmorphisme dans des espaces vectorielle de diemnsion égal à l'ordre de la matrice mais je ne peux pas t'en dire beaucoup plus...
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 27 Juin 2017, 23:35
par Matt_01 » 27 Juin 2017, 23:35
infernaleur a écrit:Salut !
Je m’intéressais à démontrer la nilpotence d'une matrice triangulaire supérieur à diagonale nulle mais je n'y parviens pas ...
Auriez-vous quelques pistes à me donner

Merci !!!
Que vaut son polynôme caractéristique ?
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 27 Juin 2017, 23:56
par infernaleur » 27 Juin 2017, 23:56
Merci pour ta réponse Viko, j'ai essayé d'y réfléchir mais je n'ai pas avancer
Merci pour votre réponse Matt_01
Je ne connaissais pas la notion de polynôme caractéristique j'ai donc regarder rapidement a quoi cela correspondais et j'ai aussi pris connaissance du théorème de Cayley-Hamilton
on à donc P(X)= X^n ( pour une matrice triangulaire supérieur stricte de taille n) où P est le polynôme caractéristique.
(On note A la matrice triangulaire supérieur stricte)
Et d'après le théorème de Cayley-Hamiton , on sait que P(A)=A^n=0
C'est cela que vous vouliez que je fasse ?
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 28 Juin 2017, 08:06
par Pseuda » 28 Juin 2017, 08:06
Bonjour,
Pour développer le message de Viko, je dirais que la matrice M d'ordre n considérée est la matrice d'un endomorphisme

dans un e-v de dim n dans une certaine base
)
(ou de l'application linéaire

de

canoniquement associée à M).
Comme M est triangulaire supérieure d'éléments diagonaux nuls, alors :
=0, u(e_2)=\alpha_{12}e_1, ... u(e_p)=\sum_{k=1}^{p-1} \alpha_{kp}e_k, ..., u(e_n)=\sum_{k=1}^{n-1} \alpha_{kn}e_k)
.
Il suffit alors de montrer que :
=0)
. On a alors
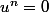
, donc
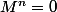
.
-
aviateur
 par aviateur » 28 Juin 2017, 10:13
par aviateur » 28 Juin 2017, 10:13
Bonjour
Pour la démo on peut le faire à la main comme le propose @pseuda. C'est un bon exercice,
Mais l'utilisation du th de Cayley Hamilton donne le résultat immédiatement.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 28 Juin 2017, 17:07
par infernaleur » 28 Juin 2017, 17:07
Daccord merci !!!
C'est bon Pseuda merci pour votre réponse très détaillé c'est cette démonstration que je cherchais.

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
