bonjour,
aide moi s'il vous plait.
Quel est la nature de cette courbe d'équation:
racine carre((x+1)/3)+racine carrée((y-7)/2)=1
j'ai essaye de poser X=racine carrée(x+1) et Y=racine carrée(y-7)
tel que x+1>=0 et y-7>=0
et je trouve X/racine carre(3) +Y/racine carree(2) :c'est une équation cartésienne d'une droite
mais quand je le fais sur un logiciel de graphe, c'est pas une droite.
merci de vos réponse.
Nature d'une courbe.
10 messages
- Page 1 sur 1
Re: nature d'une courbe.
salut
on élève au carré une première fois, simplifie et isole la dernière racine carrée
on élève au carré une seconde (donc dernière) fois et on tombe sur un polynome de degré 2 en x et y donc la courbe est une conique du plan (hyperbole, parabole, ellipse, ....)
on effectue une factorisation de Gauss pour confirmer le résultat ... et donner les éléments caractéristiques de la conique ...
on élève au carré une première fois, simplifie et isole la dernière racine carrée
on élève au carré une seconde (donc dernière) fois et on tombe sur un polynome de degré 2 en x et y donc la courbe est une conique du plan (hyperbole, parabole, ellipse, ....)
on effectue une factorisation de Gauss pour confirmer le résultat ... et donner les éléments caractéristiques de la conique ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: nature d'une courbe.
Bonjour,
il faut étudier:
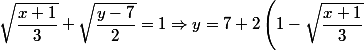^{2}=\dfrac{2}{3}x+\dfrac{29}{3}-4\sqrt{\dfrac{x+1}{3}})
il faut étudier:
Modifié en dernier par Razes le 23 Aoû 2017, 19:16, modifié 1 fois.
Re: nature d'une courbe.
ou alors
avec les conditions adéquates sur u et v .... l'équation devient
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: nature d'une courbe.
salut
A noter que si par exemple x>2 alors (x+1)/3>1 donc racine((x+1)/3)>1 et l'égalité de départ ne peut pas être vérifiée. On n'a qu'un arc de parabole
A noter que si par exemple x>2 alors (x+1)/3>1 donc racine((x+1)/3)>1 et l'égalité de départ ne peut pas être vérifiée. On n'a qu'un arc de parabole
Re: nature d'une courbe.
Bonjour chan79,
Bien vu, merci pour la remarque, il faut donc que:

Donc le tableau de variation de la fonction se réduit à:
se réduit à:
=\dfrac{2}{3}x+\dfrac{29}{3}-4\sqrt{\dfrac{x+1}{3}}; f'(x)=\dfrac{2}{3}-\dfrac{2}{\sqrt{3\left (x+1\right )}})
=0\Leftrightarrow x=2)
 & & - & 0 \\ \hline f(x) & 9 & \searrow & 7 \end{array})
Bien vu, merci pour la remarque, il faut donc que:
Donc le tableau de variation de la fonction
Re: nature d'une courbe.
c'est un arc de la parabole de foyer (-1/13;109/13) et de directrice: 3x+2y=11
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
