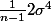cesar a écrit:on peut aussi calculer une estimation de l'écart type, mais si le meilleur estimateur de la moyenne, c'est la moyenne des données, le meilleurs estimateur de l'écart type sigma n, c'est l'écart type des données calculé en divisant par 149 au lieu de 150...
Salut Cesar.
Ce que tu dis n'est pas juste en divisant par 149 ton estimateur sera sans biais, mais ce ne sera pas un "meilleur estimateur" de l'ecart type pour autant.
En effet son erreur quadratique est superieur a celle de quand on divise par 150.
On ne juge pas la qualité d'un estimateur a son biais mais a son risque quadratique(somme pondérée des erreurs aux carrées): somme du biais et de la variance.
Et ici meme si le biais est nul il est superieur à la somme Variance plus biais obtenue en divisant par 150.
De plus le biais de la variance vaut alors
 - \sigma^2)
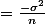
-> 0 reduisant le seul desavantage de "l'estimateur 150"(intelectuel car dans la pratique ça n'en est pas un) a néant du moment que le nombre de données et suffisamment grand
Au final la moyenne de ton erreur en divisant par 149 sera plus grande qu'en divisant par 150 meme si la moyenne de tes estimations vaut théoriquement
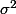
, le paramètre estimé.
En divisant par 150 la moyenne de ton erreur quadratique de ton estimateur sera plus faible, meme si la moyenne theorique de tes estimateurs ne vaudra pas
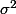
Au final l'estimateur le plus fiable est celui obtenu en divisant par 150.
i.e Si j'ai des données je me tromperai probablement de moins en estimant ma variance en divisant par 150 qu'en divisant par 149.
Malheureusement beaucoup croient que biais = qualité, ce qui est faux en general, cette confusion va jusqu'a prendre parfois un estimateur moins bon pour la variance(comme je le vois souvent par des non statisticien) ce qui est une aberration.
Toute fois, ce n'est pas si grave car les deux estimateurs sont consistants et converge a la même vitesse et la difference est negligeable quand n grandi:
risque quadratique:
de l'estimateur en divisant par n: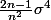 de l'estimateur en divisant par n-1:
de l'estimateur en divisant par n-1: