Moindres carrés sur une équation matricielle
48 messages
- Page 2 sur 3 - 1, 2, 3
Re: moindres carrés sur une équation matricielle
je pense que j'arriverais à le programmer mais il me faudra une bibliothèque d'algèbre linéaire comme Numpy pour Python ou Lapack pour C++ car programmer à la main la résolution d'un système à neuf équations et neuf inconnues est complexe sinon (j'utilise les déterminants pour la résolution des systèmes)
Re: moindres carrés sur une équation matricielle
j'utilise les déterminants pour la résolution des systèmes)
Pas top !
Re: moindres carrés sur une équation matricielle
j'ai écrit le code suivant en Python, ça se lit bien tu peux me dire si c'est bon ?
- Code: Tout sélectionner
import numpy as np
import random as r
N=100
A=np.zeros((3,N));#tableau de connues 3xN
B=np.zeros((3,N));#tableau de connues 3xN
#on remplit aléatoirement A et B
for i in range(3):
for j in range(N):
A[i,j]=r.random()
B[i,j]=r.random()
M=np.zeros((3,3));#tableau d'inconnues 3x3
S=np.zeros((9,9));#coefficients du système 9x9
R=np.zeros(9);#coefficients résultats du système 9
for j in range(3):
for l in range(3):
for k in range(3):
for i in range(N):
S[l+3*j,k+3*j]=S[l+3*j,k+3*j]+B[k,i]*B[l,i];
for j in range(3):
for l in range(3):
for i in range(N):
R[l+3*j]=R[l+3*j]+A[j,i]*B[l,i];
X = np.linalg.solve(S, R)
for j in range(3):
for k in range(3):
M[j,k]=X[k+3*j];
print(M)
Modifié en dernier par sylvain231 le 07 Avr 2020, 18:27, modifié 1 fois.
Re: moindres carrés sur une équation matricielle
J'aurais utilisé la fonction sum, mais ça me semble bien correspondre au système que je t'ai donné.
Re: moindres carrés sur une équation matricielle
Comment vérifier que c’est bon ? En fixant N à 1 et en faisant la multiplication matricielle ?
Re: moindres carrés sur une équation matricielle
J’ai vérifié et obtient une erreur de 0 pour N=1 c’est bon signe !
Re: moindres carrés sur une équation matricielle
Si tu prends tes  et
et 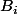 au hasard, tu ne verras pas grand chose. Mais si tu fixes
au hasard, tu ne verras pas grand chose. Mais si tu fixes  , choisis des
, choisis des 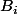 au hasard et prends des
au hasard et prends des qui sont des perturbations pas trop grandes, au hasard, des
qui sont des perturbations pas trop grandes, au hasard, des  , alors tu devrais retrouver
, alors tu devrais retrouver  .
.
Re: moindres carrés sur une équation matricielle
Pourquoi ne recherches tu pas une approximation affine en minimisant  , avec M et P à déterminer ?
, avec M et P à déterminer ?
Re: moindres carrés sur une équation matricielle
Salut,
Sinon, concernant la partie programmation, tu peut pas mal raccourcir ton code vu que le système linéaire à résoudre correspond à chercher l'inverse d'une matrice 3x3 et que numpy sait le faire directement.
Si tu note la matrice
la matrice  dont les
dont les  colonnes sont les
colonnes sont les  et
et  celle dont les colonnes sont les
celle dont les colonnes sont les 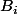 alors ta fonction à minimiser est
alors ta fonction à minimiser est  où la norme sur les matrices
où la norme sur les matrices  est la "norme 2".
est la "norme 2".
Et comme cette norme est issue du produit scalaire) la différentielle de
la différentielle de  en
en  est
est \,^t(HB)\big)) donc les points critique de
donc les points critique de  sont les
sont les  tels que
tels que \,^t\!B=0) c'est à dire
c'est à dire =A\,^t\!B) et c'est ça ton système linéaire de 9 équations à 9 inconnues.
et c'est ça ton système linéaire de 9 équations à 9 inconnues.
Ce système admet évidement une unique solution (qui est évidement ton minimum) lorsque la matrice) est inversible et dans ce cas, la solution est
est inversible et dans ce cas, la solution est ^{-1}) .
.
Remarque : si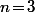 et
et  inversible, on retrouve bien évidement que la solution est
inversible, on retrouve bien évidement que la solution est  .
.
Sinon, concernant la partie programmation, tu peut pas mal raccourcir ton code vu que le système linéaire à résoudre correspond à chercher l'inverse d'une matrice 3x3 et que numpy sait le faire directement.
Si tu note
Et comme cette norme est issue du produit scalaire
Ce système admet évidement une unique solution (qui est évidement ton minimum) lorsque la matrice
Remarque : si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: moindres carrés sur une équation matricielle
voici mon code :
- Code: Tout sélectionner
print("M2=",np.matmul(A.T,np.matmul(B,np.linalg.inv(np.matmul(B.T,B)))))
Re: moindres carrés sur une équation matricielle
Ben314, j'ai l'impression que tu t'es fichu dedans en transposant du mauvais côté. Me trompé-je ?
Re: moindres carrés sur une équation matricielle
GaBuZoMeu a écrit:Ben314, j'ai l'impression que tu t'es fichu dedans en transposant du mauvais côté. Me trompé-je ?
Non, OK, ça revient bien exactement au système que j'avais écrit :
Re: moindres carrés sur une équation matricielle
Je trouve pour différentielle -2trace (t(MB-A)HB) , ce qui interdit d'isoler H .
J'y ai cru , ça aurait été trop simple. En general XY=0 ssi Im(Y) inclus dans ker(X) .
Quid de l'approximation affine ?
J'y ai cru , ça aurait été trop simple. En general XY=0 ssi Im(Y) inclus dans ker(X) .
Quid de l'approximation affine ?
Modifié en dernier par tournesol le 08 Avr 2020, 14:28, modifié 1 fois.
Re: moindres carrés sur une équation matricielle
Non non, tournesol, il faut y croire !
Soit une matrice de colonnes
une matrice de colonnes 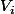 . Alors
. Alors
= \langle V;V\rangle)
Avec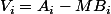 on a
on a 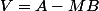 et
et =\langle V;V\rangle) . L'application linéaire tangente de
. L'application linéaire tangente de  en
en  est donc
est donc
B^{\mathsf T}H^{\mathsf T})
Soit
Avec
48 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
