Bonjour,
Je suis actuellement en dernière année d'école d'ingénieur et je rencontre des difficultés sur un projet.
Je n'ai jamais fais de moindres carrés sous contraintes et encore moins de moindres carrés non linéaires sous contraintes.
Ma problématique est la suivante :
Je place un objet 3D dans un logiciel (Autodesk Revit) "à lil". En revanche je connais les coordonnées théoriques (entachées de faibles erreurs) de certains des points de mon objet. Je cherche donc à "recaler" mon objet à la bonne position. J'ai donc pensé qu'une procédure de moindres carrés sous contraintes pouvait répondre à ma problématique.
Le problème est que je suis incapable de construire mes équations et donc mes matrices (je suis plus un programmeur qu'un mathématicien).
Admettons que j'ai 5 points dont les coordonnées théorique sont connus : Xt1, Yt1, Zt1, Xt2, Yt2, Zt3... Ces coordonnées ont été déterminées par photogrammétrie terrestre et sont entachée d'une erreur d'environ 2cm.
J'ai également les coordonnées de ces points de l'objet placé à lil : Xp1, Yp1, Zp1,...
Mon objet n'étant pas déformable j'ai donc des contraintes sur les coordonnées corrigées (mes inconnues) Xc1, Yc1, Zc1... Ces contraintes sont que la distance entre chaque point reste constante. Je n'ai pas déterminé combien de contraintes je doit poser, je dois simplement atteindre une précision meilleure que 5cm.
Exemple : sqrt[(Xc1-Xc2)²+(Yc1-Yc2)²+(Zc1-Zc2)²] = sqrt[(Xp1-Xp2)²+(Yp1-Yp2)²+(Zp1-Zp2)²] = d12 pour faire plus simple.
Cela semble donc être une procédure de moindres carrés sous contraintes non linéaires. Chose que je n'ai jamais eu l'occasion d'aborder en cours. J'ai seulement pu aborder des moindres carrés linéaires et non linéaires classiques, ainsi que des moindres carrés implicites.
Si quelqu'un pouvait me guider dans la formation de mes équations et donc de mes matrices, cela m'aiderait énormément dans mon travail de recherche.
Merci d'avance
Jordi
Moindres carrés non linéaire sous contraintes
12 messages
- Page 1 sur 1
Hello,
Je me trompe peut-être, mais personnellement je trouve assez complexe d'optimiser sur la position des points directement alors justement qu'ils sont contraints, avec en plus un nombre assez énormes de contraintes (tu as je suppose n points, et donc a priori n² contraintes).
J'aurais plutôt vu un moyen de paramétrer la position de tes points de telle sorte de supprimer les contraintes (qu'elles soient intrinsèques à la paramétrisation). C'est-à-dire concrètement de positionner l'objet par une position, et une matrice de rotation. La position c'est 3 paramètres, et la matrice de rotation 3 de plus (tu peux l'écrire avec les 3 angles d'Euler autour de chaque axe, par exemple).
Ainsi chacun de tes points peut s'écrire P' = G + RP, où P' est la position de ton point que tu essayes de faire coller avec les valeurs théoriques, G sera la position du "centre" (ou pas à la limite, un point de référence en tout cas) de l'objet, et P la position du point dans ton référentiel de base, avant rotation.
du coup, tu as donc 6 paramètres de positionnement pour l'ensemble des points et 0 contrainte, au lieu de 3*n paramètres (les 3 coordonnées des n points) et n² contraintes. Je pense que ça va simplifier significativement le problème (ainsi que le temps de calcul). Pour autant il y a encore du travail pour mettre en place les moindres carrés !
Damien
Je me trompe peut-être, mais personnellement je trouve assez complexe d'optimiser sur la position des points directement alors justement qu'ils sont contraints, avec en plus un nombre assez énormes de contraintes (tu as je suppose n points, et donc a priori n² contraintes).
J'aurais plutôt vu un moyen de paramétrer la position de tes points de telle sorte de supprimer les contraintes (qu'elles soient intrinsèques à la paramétrisation). C'est-à-dire concrètement de positionner l'objet par une position, et une matrice de rotation. La position c'est 3 paramètres, et la matrice de rotation 3 de plus (tu peux l'écrire avec les 3 angles d'Euler autour de chaque axe, par exemple).
Ainsi chacun de tes points peut s'écrire P' = G + RP, où P' est la position de ton point que tu essayes de faire coller avec les valeurs théoriques, G sera la position du "centre" (ou pas à la limite, un point de référence en tout cas) de l'objet, et P la position du point dans ton référentiel de base, avant rotation.
du coup, tu as donc 6 paramètres de positionnement pour l'ensemble des points et 0 contrainte, au lieu de 3*n paramètres (les 3 coordonnées des n points) et n² contraintes. Je pense que ça va simplifier significativement le problème (ainsi que le temps de calcul). Pour autant il y a encore du travail pour mettre en place les moindres carrés !
Damien
j'ai pensé à ça, le problème, c'est qu'il faut creuser et que je n'ai peut être pas les compétences nécessaires:
cinq points sont connus avec précision. On suppose qu'on peut en extraire
un repère affine (=tétraèdre en dimension 3).
ça donne, puisque il y a les contraintes du solide, des positions certaines (mais non effectives
car entachées d'erreur, pour tous les points du solide)
on dit ensuite que les points se répartissent autour de leur position certaine selon la loi normale
et on programme un test H0 contre H1, pour déterminer
si une configuration donnée de points est acceptable ou non. Il s'agit donc de la conjonction
de n gaussiennes.
cinq points sont connus avec précision. On suppose qu'on peut en extraire
un repère affine (=tétraèdre en dimension 3).
ça donne, puisque il y a les contraintes du solide, des positions certaines (mais non effectives
car entachées d'erreur, pour tous les points du solide)
on dit ensuite que les points se répartissent autour de leur position certaine selon la loi normale
et on programme un test H0 contre H1, pour déterminer
si une configuration donnée de points est acceptable ou non. Il s'agit donc de la conjonction
de n gaussiennes.
Merci pour vos réponses rapides.
-> DamX : Niveau temps de calcul je ne pense pas que ce soit un gros problèmes étant donné que je n'ai que quelques points pour un objet, ça dépasse rarement la dizaine. En revanche niveau complexité du système ça peut en effet devenir compliqué. Je vais continuer de creuser. Aussi mes compétences en maths étant limitée, la piste que tu mentionne serait elle une similitude sans facteur d'échelle ? Je suis tombé sur une solution mentionnant cela dans la matinée mais je me demandais si cela était vraiment possible du fait que j'ai des erreur de l'ordre de 2cm sur mes points de calage. Si j'ai bien compris ce que tu me conseille c'est prendre le problème sous l'angle de la similitude : mes équations sont donc des similitudes et j'effectue les moindres carrés sur ces équations. Je m'affranchit ainsi des contraintes. C'est cela ?
-> mathelot : je pense que je n'ai malheureusement pas les compétences non plus. Je creuserai tout de même si j'épuise mes autres pistes. Merci beaucoup.
Jordi
-> DamX : Niveau temps de calcul je ne pense pas que ce soit un gros problèmes étant donné que je n'ai que quelques points pour un objet, ça dépasse rarement la dizaine. En revanche niveau complexité du système ça peut en effet devenir compliqué. Je vais continuer de creuser. Aussi mes compétences en maths étant limitée, la piste que tu mentionne serait elle une similitude sans facteur d'échelle ? Je suis tombé sur une solution mentionnant cela dans la matinée mais je me demandais si cela était vraiment possible du fait que j'ai des erreur de l'ordre de 2cm sur mes points de calage. Si j'ai bien compris ce que tu me conseille c'est prendre le problème sous l'angle de la similitude : mes équations sont donc des similitudes et j'effectue les moindres carrés sur ces équations. Je m'affranchit ainsi des contraintes. C'est cela ?
-> mathelot : je pense que je n'ai malheureusement pas les compétences non plus. Je creuserai tout de même si j'épuise mes autres pistes. Merci beaucoup.
Jordi
Quelque chose de la forme B=AX
Xt-Xp Tx 1 0 0 0 Yp -Zp
B= Yt-Yp Ty A= 0 1 0 Zp 0 -Xp
Zt-Zp Tz 0 0 1 -Yp Xp 0
X= Ex
Ey
Ez
Et ce pour chaque point, Tx Ty Tz étant mes translations, Ex Ey Ez mes rotations, Xt X théorique, Xp X placé etc...
Ça donne un système de moindres carrés linéaires, et ça je sais faire !
Merci beaucoup, je n'avais pas pensé à ça alors que je m'en suis déjà servi...
Jordi
Xt-Xp Tx 1 0 0 0 Yp -Zp
B= Yt-Yp Ty A= 0 1 0 Zp 0 -Xp
Zt-Zp Tz 0 0 1 -Yp Xp 0
X= Ex
Ey
Ez
Et ce pour chaque point, Tx Ty Tz étant mes translations, Ex Ey Ez mes rotations, Xt X théorique, Xp X placé etc...
Ça donne un système de moindres carrés linéaires, et ça je sais faire !
Merci beaucoup, je n'avais pas pensé à ça alors que je m'en suis déjà servi...
Jordi
pas sûr d'avoir suivi, si tu remplaces les coordonnées de tes points par les translations rotations et que tu optimises dessus, ça n'avance pas à grand chose, tu as juste exprimé les coordonnées différemment.
Ce que je proposais était de n'utiliser que les translations/rotations pour le centre de l'objet, qui sont tes paramètres (6 paramètres donc), et tous les points de l'objet sont définis de manière fixée par rapport au centre dans le repère d'origine, ce qui retranscrit intrinsèquement toutes tes contraintes. Du coup le problème se ramène à une optimisation à 6 degrés de libertés sans contraintes. Peut-être est-ce bien ce que tu as compris mais ta formulation ("et ce pour chaque point") me laissait des doutes.
Ce que je proposais était de n'utiliser que les translations/rotations pour le centre de l'objet, qui sont tes paramètres (6 paramètres donc), et tous les points de l'objet sont définis de manière fixée par rapport au centre dans le repère d'origine, ce qui retranscrit intrinsèquement toutes tes contraintes. Du coup le problème se ramène à une optimisation à 6 degrés de libertés sans contraintes. Peut-être est-ce bien ce que tu as compris mais ta formulation ("et ce pour chaque point") me laissait des doutes.
On note :
-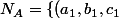, ..., (a_n, b_n, c_n)\}) l'ensemble des points "placé à l'oeil",
l'ensemble des points "placé à l'oeil",
-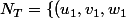, ..., (u_n, v_n, w_n)\}) l'ensemble des points théoriques et
l'ensemble des points théoriques et
-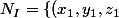, ..., (x_n, y_n, z_n)\}) l'ensemble des points recherchés (ou inconnues)
l'ensemble des points recherchés (ou inconnues)
on cherche alors a minimiser la somme des distances entre chaque couple de points :
[CENTER]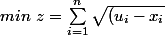^2+(v_i-y_i)^2+(w_i-z_i)^2}) [/CENTER]
[/CENTER]
sous contraintes que l'on préserve les distances entre tous les couples de points :
[CENTER]^2 + (y_i - y_j)^2 + (z_i - z_j)^2} = \sqrt{(a_i - a_j)^2 + (b_i - b_j)^2 + (c_i - c_j)^2} \ \ \ \ \forall i = 1..n, \ \ \ \ \forall j = 1 .. n, \ \ \ \ i \ne j) [/CENTER]
[/CENTER]
se résout avec excel :zen:
-
-
-
on cherche alors a minimiser la somme des distances entre chaque couple de points :
[CENTER]
sous contraintes que l'on préserve les distances entre tous les couples de points :
[CENTER]
se résout avec excel :zen:
DamX -> Mon message ne ressemble à rien car je ne l'ai pas visualisé avant de le poster, j'avais organisé mes variables en matrice. DamX nous sommes d'accord. C'est simplement une transformation de Bursa Wolf que l'on peut par exemple retrouver en géodésie. J'ai écris la quasi totalité de mon code, il me reste à trouver comment on applique cette transformation dans Revit mais ce logiciel gère les système de coordonnées d'une façon assez atypique. Je ne pourrais donc pas tester mon code de suite. Aussi je n'ai pas accès au centre de l'objet, seulement à son point de base à partir duquel il à été conçu. Mais je suis assez confiant pour le résultat. Dans tout les cas mon problème mathématique est résolu, ce n'est qu'un problème logiciel maintenant.
Cliffe -> J'ai déjà tout écris en C# mais je garde ton conseil sous le coude on ne sait jamais. Merci
Jordi
Cliffe -> J'ai déjà tout écris en C# mais je garde ton conseil sous le coude on ne sait jamais. Merci
Jordi
Pour récupérer mes coordonnées "non corrigées" je dois les pointer dans mon logiciel. Je code ça au travers d'une API que je connais peu ce qui fait que je connais mal toutes les procédures à utiliser, notamment pour l'écriture de ma transformation géométrique telle que mon logiciel peut la comprendre, ainsi qu'à quoi l'appliquer (la géométrie de mon objet ? seulement son point de base ?...). Autant de question qui ne sont pas des questions mathématique. Je pense la procédure de moindres carrés que j'ai codé solide car je l'ai déjà utilisé pour trouver une transformation locale entre deux systèmes de coordonnées Français (NTF et RGF93).
Mais bon je sais que je suis pas forcément à l'abri de tomber sur un os étant donné que je ne maîtrise encore pas bien les outils qui sont à ma disposition.
Jordi
Mais bon je sais que je suis pas forcément à l'abri de tomber sur un os étant donné que je ne maîtrise encore pas bien les outils qui sont à ma disposition.
Jordi
Salut,
Ca me rappelle un truc du temps où je préparais l'agrégation:
https://www.i2m.univ-amu.fr/~franck.boyer/Enseignement/Agreg/procuste.pdf
Après, je n'ai peut-être pas bien compris ta modélisation.
Cordialement
Ca me rappelle un truc du temps où je préparais l'agrégation:
https://www.i2m.univ-amu.fr/~franck.boyer/Enseignement/Agreg/procuste.pdf
Après, je n'ai peut-être pas bien compris ta modélisation.
Cordialement
SLA -> L'énoncé correspond à un problème très similaire au mien. En revanche je n'ai clairement pas le niveau mathématique pour suivre la démonstration. Néanmoins je retrouve des expressions identiques au miennes donc j'ai l'impression que c'est le même traitement, avec une analyse plus poussée. Merci
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
