Module et argument de (1+i)e^ipi/2

[LennySacha]

Bonjour à tous,

je dois déterminer le module et l'argument de (1+i)e^ipi/2

Pouvez-vous me mettre sur la bonne voie?

Je pensais d'abord mettre cela sous forme algébrique, la formule exp(i*theta)= cos(theta)+isin(theta) fonctionne dans mon cas?

je vous remercie

[pascal16]

soit :
met (1+i) sous forme trigo
fais la multiplication sous forme trigo (produit des modules, somme des arguments, enlever 2pi si nécessaire)
tu auras un complexe sous forme trigo
passe à la forme algébrique

soit, plus long :
met e^ipi/2 sous forme algébrique
fais la multiplication sous forme algébrique (a+ib)(c+id) = ac-bd + i (....)
repasser à la forme trigo (c'est là que c'est plus long)

[vejitoblue]

salut, je vais te donner ça mais attends la confirmation je suis pas sur:

|x||y|=|xy| et on a |e^ix|=1 pour tout x R (vu que cos²x+sin²x =1 et z complexe |z|=
et |1+1i|=

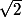
[LennySacha]

Bonjour pascal,

donc selon la première méthode j'ai maintenant:

racine de 2(cos pi/4 + isin pi/4)*e^ipi/2 c'est bien ça?

Comment dois-je procéder pour effectuer la multiplication sous forme trigo?

[LennySacha]

Ok c'est résolu merci pour vos réponses