Méthode de Richardson

[Aispor]

Bonjours,
j'ai un problème calculatoire pour cet exercice :



La réponse à la question 1 est :


Pour la question 2 :
Le choix de Richardson est de prendre
Posant
On a

et

Les solutions du polynôme caractéristique de B sont :

D'où

Je cherche à étudier lorsque
Je ne vois pas comment trop mis prendre, vu qu'il y a un maximum, 2 valeurs paramètres, et et en plus des valeurs absolu x)

Merci d'avance

[Ben314]

Salut,
Ben c'est bête comme choux : dire que le plus grand de deux nombres est <1, ça veut exactement dire qu'ils sont tout les deux <1.
Et dire que la valeur absolue d'un truc est <1, ça signifie que le truc est entre -1 et 1.

Bref, ton rayon spectral est <1 lorsque et

[Aispor]

Ah oui mince ^^
Du coup j'ai trouvé que les trois méthodes convergent pour

Pour Jacobi :

Pour Gauss-Seidel :

Il est clair que Gauss-Seidel converge plus vite que Jacobi, mais pour comparer à Richardson encore une fois la valeur me dérange

[Aispor]

Finalement voici ce que j'ai réussis à faire :

Fixant
Je cherche le paramètre qui optimise le rayon spectral de Richardson,
Pour cela, je fais un petit dessin :

pour



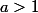
Donc

Et "Par symetrie" (argument que je ne vois pas comment bien justifié ^^

C'est Pareil si

Et l'ordre de convergence est :
1. Gauss-Seidel
2. Jacobi et Richardson

Qu'en pensez-vous ? Et pour l'argument à justifier ? Merci =)

[Ben314]

Perso., ça me semble parfaitement correct en tout cas en ce qui concerne le meilleur alpha à prendre pour la méthode de Richardson (comme j'y connais rien en analyse numérique, je sais pas à quoi ça correspond les deux autres noms de méthodes).
Et concernant le "par symétrie" du cas a<-1, ça me semble suffisant comme argument. Si tu pense que ça l'est pas, ben il te suffit de faire de nouveau le dessin dans ce cas là (qui va évidement être le même à symétrie par rapport à l'axe des ordonnées près) pour justifier que de nouveau, le alpha optimum, c'est 1/a.
Ou alors, tu écrit un truc de ce style :
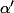
Si on pose alors on a donc le qui minimise c'est l'opposé du qui minimise .

[Aispor]

Ah oui merci Ben pour la justification =)

[aviateur]

Bonjour
@ben: (de mémoire) pour résoudre un système Ax=b par une méthode itérative on pose A=M+N avec M facilement inversible. Le système devient alors Mx=-Nx+b ou encore
On pose et
d'où la suite qui va converger vers la solution pourvu que le rayon spectral de G soit<1.
Jacobi correspond à prendre M= la diagonale de A.
Gauss-Seidel est une amélioration de Jacobi qui consiste à prendre M=D+ la partie supérieure de A. Attention néanmoins il y a des cas où Gauss-Seidel converge - vite que Jacobi.

[Aispor]

Oui on a juste vu que pour les matrices tridiagonales la rayon de Gauss est égal au carré de celui d Jacobi

[aviateur]

Oui on a juste vu que pour les matrices tridiagonales la rayon de Gauss est égal au carré de celui d Jacobi

ça ne me dit rien. Mais c'est possible. L'idée de la démo
c'est quoi?

[Aispor]

Pas fait ^.^'
Mais on le constate ça convainc assez bien xD

[aviateur]

Pour un matheux, je préfère mieux que constater! Faire une démo c'est indispensable.
Alors on pourrait poser la question en énigme.