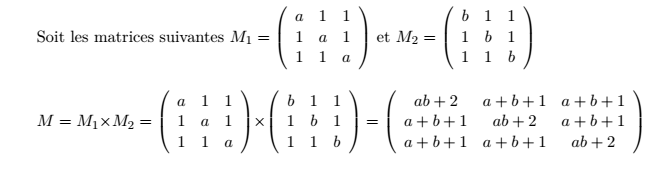Méthode calcul déterminant matrice avec paramêtre

[novicemaths]

Bonsoir

Pourriez-vous s'il vous plaît vérifier les calculs ci-dessous.


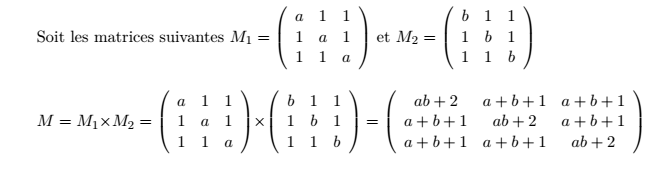
Je cherche le déterminant de M


Je pense que la règle de sarrus sera un peu hasardeuse dans cette situation.

Je pourrais utiliser la méthode traditionnelle mais ce sera long à calculer.

J'ignore si la vidéo ci-dessous peut m'aider, on parle de manipulation des colonnes de matrice pour le calcul de déterminant.

https://www.youtube.com/watch?v=ibKDAQn ... 2Q&index=8

A bientôt

[GaBuZoMeu]

Bonjour,

Le déterminant d'un produit de matrices (carrées, de même taille) est égal au .... Je suis sûr que tu connais ça.
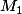
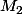
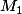
Autant l'appliquer ici. Le déterminant de est tout de même plus simple à calculer que celui de . Et pour le déterminant de quand on a calculé celui de , il suffit de remplacer par .

[novicemaths]

Bonsoir

Le déterminant d'un produit de matrices de même taille est égal au produit des déterminants des matrices carrées de même taille.

Soit

Ais-je bien résumé ?

A bientôt

[novicemaths]

Bonsoir

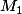
Voici le calcul de déterminant et



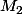
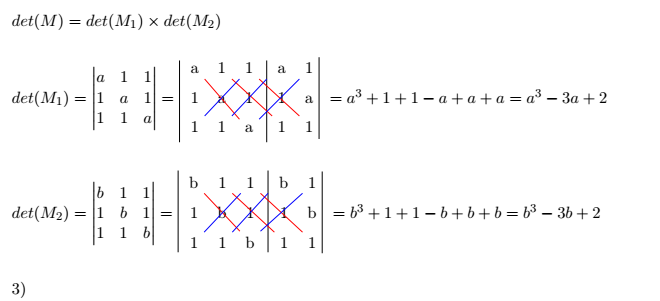
Est ce que on en conclure que a=b=0 ?

A bientôt

[GaBuZoMeu]

Comme je l'ai déjà écrit, le deuxième calcul est complètement inutile. Il suffit de remplacer a par b.
Par ailleurs il est facile de factoriser les deux déterminants.

Est ce que on en conclure que a=b=0 ?

Euh ... Peux-tu reformuler ta question de manière compréhensible ?

[novicemaths]

Bonsoir



Est-ce que c'est factoriser ?

Comment est-il possible de démontrer que b=0

A bientôt

[GaBuZoMeu]

Non, ce n'est pas factoriser. Factoriser, c'est écrire comme produit de facteurs (ici, du premier degré).

Démontrer que b= 0 ????
Si tu as une question d'énoncé, recopie-la précisément. Ici, ta question n'a aucun sens.

[novicemaths]

Bonjour

Pour la factorisation, je propose

On me demande de déduire les valeurs de a et de b.

A bientôt

[GaBuZoMeu]

Ce n'est toujours pas une factorisation. Ici, factoriser revient à trouver les racines du polynôme.

"Déduire les valeurs de a et b" n'a aucun sens tel quel. Tu dois oublier une partie de l'énoncé.

[novicemaths]

Bonsoir

Concernant la factorisation de . Est-ce que c'est cela ?

A bientôt

[Ben314]

Salut,
C'est une factorisation, mais pas "la meilleure" (i.e. en facteurs irréductibles) vu que ton deuxième terme est encore (facilement) factorisable.

[novicemaths]

Re bonsoir

Je réduis

A bientôt