Matrices inversibles

par **goudou** » 14 Juin 2009, 13:54

Bonjour à tous !
J'ai un petit soucis.
Je ne comprends pas du tout comment on montre qu'une matrice est inversible, ni comment on trouve son inverse.

J'ai regardé des sujets d'annales et cette question revient souvent. Dans mon cours on a dit que la matrice A est inversible
et son inverse est B si AB=BA=In.
Ou si A=Mat(u,B1,B2) si u est un isomorphisme
Ou (et là je ne comprends pas) si les vecteurs colonne de A forment une base.

On a fait seulement quelques applications et je ne comprends vraiment pas.
Je précise aussi que j'ai recherché sur internet avant de poser, et que je n'ai pas vu la méthode du déterminant.

Quelqu'un peut il me donner une méthode type pour montrer qu'une matrice est inversible et quelle est son inverse svp ? :hein:

par **Nightmare** » 14 Juin 2009, 14:02

Salut :happy3:

Cela dépend un peu de ta matrice mais ce qu'on peut faire (en dimension finie évidemment) pour montrer qu'une matrice est inversible est de montrer que son noyau est réduit à {0}. Cela revient à résoudre le système d'équation MX=0 (où M est ta matrice et X un vecteur colonne). Si l'unique solution de ce système est le vecteur nul alors ta matrice est inversible.

Concernant les colonnes :

Une matrice c'est un représentant d'un endomorphisme dans des bases. On sait qu'une application linéaire est uniquement déterminée par les images des éléments de la base. (Par exemple une application linéaire sur R² est exactement determinée par les images de (0,1) et (1,0))
Ainsi la matrice est simplement un tableau qui a pour but de représenter les images des vecteurs de base dans la deuxième base, ce qui suffit pour décrire l'endomorphisme.

Une matrice est inversible lorsque l'endomorphisme est bijectif. On se rend compte que c'est le cas si et ssi l'endomorphisme envoie une base sur une base. Or on connait les images de la base, ce sont les vecteurs colonnes de la matrice. Ainsi l'endomorphisme est bijectif, et donc la matrice est inversible, si et ssi les vecteurs colonnes de la matrice sont une base.

par **goudou** » 14 Juin 2009, 14:35

Je ne suis pas sûre d'avoir compris pour la première méthode, alors je me permets de réexpliquer comme je l'ai compris

Prenons la matrice A= a b c
..............................d e f
..............................g h i
Il faut donc prendre X=x1, et chercher AX=0?
...............................x2
...............................x3
Et la matrice est inversible si X=0?
...........................................0
...........................................0

Ensuite, si elle l'est, pour trouver l'inverse, peut on opérer comme cela : ?
Soit B la matrice inverse
AB=A* a' b' c' = 1 0 0
...........d' e' f' . 0 1 0
...........g' h' i' . 0 0 1
Puis, on résout le système que l'on va trouver ...

(Désolée pour l'écriture des matrices !!)

par **Nightmare** » 14 Juin 2009, 14:47

Oui c'est bien ça pour l'inversibilité, sauf que pour trouver l'inverse on ne va pas chercher à résoudre ce système. Plusieurs méthodes existent, tu peux les trouver sur internet. Par exemple on peut par combinaisons linéaires sur les lignes ou les colonnes passer d'une matrice inversible à la matrice identité. Le produit des matrices représentant ces combinaisons (matrices dites élémentaires) forme donc exactement l'inverse de la matrice.

par **goudou** » 14 Juin 2009, 15:44

Les méthodes que je trouve prennent toutes en compte le déterminant !

par **Nightmare** » 14 Juin 2009, 15:47

Pour montrer l'inversibilité d'accord mais pour calculer l'inverse cela m'étonnerait qu'on te propose des méthodes avec le déterminant (à part pour les matrices 2x2 ou 3x3).

Regarde cette page par exemple.

par **goudou** » 14 Juin 2009, 15:51

Non, pas moyen, je trouve soit une méthode avec le déterminant, soit ce sont des gens qui demandent un algorithme pour programmer le calcul de l'inverse d'une matrice !

par **goudou** » 14 Juin 2009, 15:54

Qu'entends tu par combinaison linéaire des lignes ou des colonnes ?

par **Nightmare** » 14 Juin 2009, 15:55

Il ne me semble pas que la page que je t'ai donnée parle de déterminant.

par **goudou** » 14 Juin 2009, 15:56

Oh désolée je n'avais pas vu ton lien ! Je vais y jeter un oeil tout de suite =)

par **Ptiboudelard** » 14 Juin 2009, 19:39

Bonsoir !!!

Pourquoi n'utilises tu pas la résolution par système de Gauss ?

Tu poses AX=X' où A est la matrice à inverser,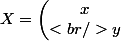

et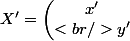

Tu mets tout sous forme de système, puis tu essaies de triangulariser le système. Une fois que tu as obtenu le système triangulaire tu regardes les pivots. Si aucun pivot n'est nul alors c'est un sytème de Cramer. La matrice est donc INVERSIBLE est son inverse est : et là tu résouds le système en fonction de x', y'

Les coefficients devant le x' et le y' seront les valeurs dans la matrice inverse !

N.B: le nombre de valeurs dans la colonne de la matrice X et X' est fonction du nombre de colonne de la matrice à inverser

par **Nightmare** » 14 Juin 2009, 20:05

Une autre technique parfois très efficace pour inverser une matrice est d'en trouver un polynôme annulateur (pourvu que la taille de la matrice ne soit pas trop grande, on peut se contenter du polynôme caractéristique)

par **Ptiboudelard** » 14 Juin 2009, 20:17

Ah je ne connais pas cette méthode ! Peux tu l'expliquer un peu plus en détails ? Merci d'avance ;-)

par **Nightmare** » 14 Juin 2009, 20:28

Eh bien une fois qu'on a un polynôme annulateur de M rien de plus simple :

Si

(avec

non nul puisque M est inversible)

On a donc :

l'inverse de M n'est donc rien d'autre que

:happy3:

par **Ptiboudelard** » 15 Juin 2009, 04:33

Ah d'accord ! Juste, comment fait on pr determiner le polynome ??

par **trocho** » 15 Juin 2009, 07:45

Sinon, il y a la fameuse formule immangeable...

L'inverse de la matrice A est égal à la transposée de la comatrice de A dont tous les coefficients sont divisées par le déterminant de A.

(Je faisais comme ça en L1, j'étais bien content de trouver d'autres méthodes par la suite :marteau: )

par **Nightmare** » 15 Juin 2009, 10:22

Ptiboudelard a écrit:Ah d'accord ! Juste, comment fait on pr determiner le polynome ??

Le théorème de Cayley-Hamilton affirme que le polynôme caractéristique d'une matrice (c'est à dire le polynôme P=det(M-XI)) en est un polynôme annulateur. Sinon le calcul des puissances successives de la matrice fait des fois apparaitre des choses sympathiques.

par **goudou** » 15 Juin 2009, 13:22

Désolée de ne pas avoir répondu plus tôt, j'ai eu un petit soucis de connexion

Bon pour trouver l'inverse, je ne comprends toujours pas :(

J'arrive à dire si elle est inversible ou pas par la méthode du vecteur colonne, mais après je ne comprends pas comment poursuivre.

J'ai continué de bosser sur les annales, et je me permets de vous présenter le sujet.
"Pour chacune des matrices suivantes, étudier si elle est inversible et si oui, calculer sa matrice inverse :

A=1 1 -1
....0 1 0
....1 2 -1

B=2 1 -1
....0 1 0
....1 -1 2"

Par la méthode du vecteur colonne, je trouve que A n'est pas inversible, car on ne conclut pas que x1=x3=0. (pour X=(x1,x2,x3))
Je trouve par contre que la matrice B est inversible. Mais à partir de là, je ne comprends pas comment on trouve l'inverse.

par **Nightmare** » 15 Juin 2009, 13:44

Fais un effort, tout est expliqué dans le lien que je t'ai donné!

par **goudou** » 15 Juin 2009, 14:03

Je ne comprends pas ces histoires de lignes que l'on inverse !
Enfin comment procède t-on. Que veulent ils dire? D'abord il faut regarder si il existe i>=k, tel que a(ik) différent de 0, et échanger les lignes, puis pour i allant de 1 à n, encore inverser des lignes ?
Je suis totalement perdue !

Matrices inversibles

Matrices inversibles

Qui est en ligne