Je peux utiliser pour le log la série entière ^{n+1}\frac{A^n}{n}})
mais elle ne converge pas normalement pour n'importe quelle matrice, y'a pas un problème de continuité alors pour le DL ?De définir le log matriciel pas
\!=\!\sum_{n\geq 1}\frac{(-1)^{n+1}}{n}A^n)
, ça marche.
La série converge normalement pour les matrices
telles que
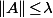
pour toute constante
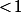
(avec n'importe quelle norme matricielle subordonnée, donc telle que
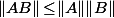
) donc c'est parfaitement continu au voisinage de
.
Le seul inconvénient, c'est qu'avec "que ça" comme définition, ça ne permet de calculer que des log de matrices proche de
, mais vu ce que tu compte en faire, c'est pas gênant.
Oui : tu peut faire le pr
Pour montrer que M^n=exp(nln(M)), je peux montrer que exp composée avec ln vaut la matrice identité en posant le produit des deux séries.Oui.
Est-ce que à partir de ce moment les règles des DL sont les mêmes que pour ceux des fonctions continues et dérivables infiniment ? Oui et non.
Là tu as deux façons de faire des D.L. : soit la façon "normale" pour des fonctions entre espaces vectoriels normés (sans plus) consistant à utiliser les différentielles successives de ta fonction qui donne des trucs du style
=f(A)+d_f(A).H+d_f^2(A).H.H+\cdots)
où
)
est une application linéaire de
)
dans lui même et
)
est une application
bilinéaire de
\!\times\!{\mathcal M}_n(\K))
dans
,
)
est trilinéaire, etc . . .
Soit tu veut un truc qui ressemble plus au D.L. qu'on fait dans
c'est à dire quelque chose du style
=a_0+a_1H+a_2H^2+\cdots)
où
doit évidement être une matrice (éventuellement nulle comme dans le log çi dessus), mais c'est pas trop clair si les autres
doivent être des réels ou des matrices.
Sauf que ce cas de figure, c'est plus que très très rare que tu l'ait, même avec des fonctions
archi simples vu que même avec un bête polynôme tu peut pas écrire ce type de relation à cause de la non commutativité du produit matriciel :
^2=A^2\!+AH+HA+H^2)
et, à moins que
et
commutent, tu ne peut pas "résumé" le
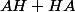
à un simple
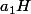
quel qu'il soit.
Bref, sauf cas très très particulier, comme celui de l'exponentielle en 0 ou du logarithme en I, tu n'a pas de D.L. de cette forme là.
Pour montrer que la partie de gauche converge bien j'utilise la formule du binôme de Newton et je majore le terme de la somme.J'ai pas compris s'il y avait une question là...
Puisque A est diagonalisable, on peut utiliser le critère de densité des matrices diagonalisables dans Mn(K) pour généraliser la propriété à toutes les matrices ? Et dans la décomposition de Jordan, I c'est une matrice diagonale ou la matrice identité ?J'ai pas bien compris la question.
Sauf éventuellement le fait que, pour pouvoir faire de l'analyse (i.e. des limites et donc des sommes de séries), il faut que le corps de base
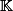
ça soit
ou
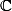
et pas autre chose. Et que si on veut que les matrices diagonalisables soient dense dans l'ensemble des matrices, ben là il faut que
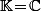
vu que c'est faux dans
.
