Matrice et sous espace vectoriel

[Licencegc]

Bonjour à tous,

J'ai comme système de solutions :
x = -2m^2+m
y = m+1
z = -2m-1

On me demande : Pour quelle valeur de m l'ensemble des solutions est-il un sous-espace vectoriel de R^3 ?
Je ne trouve pas de méthode pour résoudre cette question.
En cherchant j'ai trouvé que : W est un sous espace vectoriel ssi :
--> le vecteur 0 appartient à W
--> les vecteurs u et v appartiennent à W alors leur somme appartient à W
--> k scalaire quelconque et si le vecteur u appartient à W, alors ku appartient à W
Or comment définit-on W a partir de mon système de solutions?
Je ne sais s'il faut passer par là ou s'il y a quelque chose de plus évident.
Merci de votre aide.

[LB2]

Bonjour,

tu disposes d'une équation paramétrique de W (en fonction de m). (sous réserve qu'elle soit correcte)

Procédons par condition nécessaire : à quelle condition sur m, W contient-il le vecteur nul de R^3 ?

[GaBuZoMeu]

Réponse : jamais, car un sous-espace vectoriel de 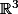contient toujours .

Mais cette question paraît stupide parce que tu as sans doute mal interprété l'énoncé. Seulement, comme tu nous caches l'énoncé, on ne peut pas savoir comment remettre les choses d'aplomb.

[Licencegc]

W contient le vecteur nul de R^3 à condition que :
x = -2m²+m =0
y = m+1 = 0
z = -2m -1 =0 ?

[Licencegc]

La question mon sujet est : Pour quelle valeur de m l'ensemble des solutions est-il un sous-espace vectoriel de R^3 ? (à partir du système au-dessus)

[LB2]

W contient le vecteur nul de R^3 à condition que :
x = -2m²+m =0
y = m+1 = 0
z = -2m -1 =0 ?

Oui, et donc quelles sont les valeurs possibles de m ?

[LB2]

La question mon sujet est : Pour quelle valeur de m l'ensemble des solutions est-il un sous-espace vectoriel de R^3 ? (à partir du système au-dessus)

Ça tu l'as déjà dit mais ce n'est pas un système d'équations que tu as fourni, juste une description de l'ensemble des solutions. Cette description peut être fausse si tes calculs sont faux

[Licencegc]

Mes calculs ont été vérifié par le professeur.

En résolvant le système je ne comprends pas car il n'y a aucune valeurs de m possibles puisque pour x m = 0 ou 1/2 ; pour y m = -1 ; pour z m=-1/2

[LB2]

L'ensemble vide existe en mathématiques! Démontrer qu'une équation n'a aucune solution, c'est tout à fait courant.

[tournesol]

Mais l'ensemble vide n'est pas un espace vectoriel .

[GaBuZoMeu]

Écoute, si tu ne veux pas donner l'énoncé complet, on ne peut rien de plus pour toi !