Matrice et produit vectorielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Jan 2015, 17:05
par adamNIDO » 23 Jan 2015, 17:05
Bonjour
pouvez vous mexpliquer comment il ont fait pour obtenir le terme a droite de l'egalite
note que C la base canonique de

et que représente (un vecteur
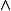
un point )


merci pour votre explication
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 23 Jan 2015, 18:02
par paquito » 23 Jan 2015, 18:02
C'est surprenant car

appaetient au noyau de A! Donc l'égalité est fausse, car le noyau de A est de dimension 1! Je ne comprends pas tout!!
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 23 Jan 2015, 18:49
par Skullkid » 23 Jan 2015, 18:49
Si u est un vecteur (en l'occurrence un vecteur colonne), la notation

désigne l'application linéaire

; d'une manière générale, f(.) est une autre notation pour la fonction f.
Pour le vecteur u = (-1,1,-1)/2 donné, la matrice de l'application en question est bien égale à la matrice A donnée. Nautrellement, u est une base du noyau de A.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Jan 2015, 18:51
par adamNIDO » 23 Jan 2015, 18:51
Skullkid a écrit:Si u est un vecteur (en l'occurrence un vecteur colonne), la notation

désigne l'application linéaire

; d'une manière générale, f(.) est une autre notation pour la fonction f.
Pour le vecteur u = (-1,1,-1)/2 donné, la matrice de l'application en question est bien égale à la matrice A donnée. Nautrellement, u est une base du noyau de A.
merci beaucoup mais si vous pouvez ajouter un peut de details
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Jan 2015, 19:02
par adamNIDO » 23 Jan 2015, 19:02
si j'ai bien compris on a en generale
soit A une matrice d'ordre 3 :
si le

alors matrice dans la base C de f associe a A est =
le produit scalaire de u contre un vecteur quelquonque de telle sorte que f(un vecteur quelquonque )
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 23 Jan 2015, 19:39
par Skullkid » 23 Jan 2015, 19:39
adamNIDO a écrit:si j'ai bien compris on a en generale
soit A une matrice d'ordre 3 :
si le

alors matrice dans la base C de f associe a A est =
le produit scalaire de u contre un vecteur quelquonque de telle sorte que f(un vecteur quelquonque )
Je ne comprends rien à ce que tu écris...
Il n'y a pas de détails à ajouter à mon post... on prend le vecteur u = (-1,1,-1)/2 exprimé dans la base canonique, on prend l'application f définie par f(x) = u ^ x et on écrit sa matrice dans la base canonique.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Jan 2015, 21:20
par adamNIDO » 23 Jan 2015, 21:20
Skullkid a écrit:Je ne comprends rien à ce que tu écris...
Il n'y a pas de détails à ajouter à mon post... on prend le vecteur u = (-1,1,-1)/2 exprimé dans la base canonique, on prend l'application f définie par f(x) = u ^ x et on écrit sa matrice dans la base canonique.
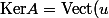 \Longrightarrow A=mat_C\left( u\wedge . \right))
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 23 Jan 2015, 22:57
par Doraki » 23 Jan 2015, 22:57
Non, une application linéaire n'est pas complètement déterminée par son noyau
mais où vas-tu chercher ça ....
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Jan 2015, 23:35
par adamNIDO » 23 Jan 2015, 23:35
Doraki a écrit:Non, une application linéaire n'est pas complètement déterminée par son noyau
mais où vas-tu chercher ça ....
cest just un proposition parceque je sais pas comment il ont fait pour avoir le terme droite de légalité
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 24 Jan 2015, 10:06
par jlb » 24 Jan 2015, 10:06
salut
(-1;1;-1) ^ (x;y;z) =(z+y;-x+z;-y-x) et ensuite tu compares avec le produit de A et du vecteur sous forme colonne (x;y;z)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 24 Jan 2015, 10:06
par adamNIDO » 24 Jan 2015, 10:06
Bonjour,
si quelqu'un peut m'expliquer comment peut on obtenir a le terme droite de l'egalite basent sur le terme a gauche
here is another one

merci pour votre aide
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 24 Jan 2015, 10:19
par adamNIDO » 24 Jan 2015, 10:19
jlb a écrit:salut
(-1;1;-1) ^ (x;y;z) =(z+y;-x+z;-y-x) et ensuite tu compares avec le produit de A et du vecteur sous fromr colonne (x;y;z)
merci mais je veux commencer par le terme a gauche et arrive a droite d'une facon détaillé
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 24 Jan 2015, 10:36
par jlb » 24 Jan 2015, 10:36
adamNIDO a écrit:merci mais je veux commencer par le terme a gauche et arrive a droite d'une facon détaillé
tu as la réponse: la matrice A est antisymétrique ( regarde un cours sur opérateur antisymétrique!)
tu calcules A.u avec u vecteur colonne (x;y;z) et tu obtiens le produit vectoriel w^u
Il suffit d'identifier w!!!
Après savoir que (a,b,c)^(d,e,f) = (bf-ce;cd-af;ae-bd) peut être utile et ensuite un système 3 à résoudre
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 24 Jan 2015, 11:05
par adamNIDO » 24 Jan 2015, 11:05
jlb a écrit:tu as la réponse: la matrice A est antisymétrique ( regarde un cours sur opérateur antisymétrique!)
tu calcules A.u avec u vecteur colonne (x;y;z) et tu obtiens le produit vectoriel w^u
Il suffit d'identifier w!!!
Après savoir que (a,b,c)^(d,e,f) = (bf-ce;cd-af;ae-bd) peut être utile et ensuite un système 3 à résoudre
=\textrm{mat}_{\mathcal{C}} \left( \frac{\sqrt{3}}{2} \left[ \frac{1}{\sqrt{3}} \begin{pmatrix}-1\\1\\-1\end{pmatrix} \right]\wedge\ . \right))
donc vous avez dit je vais commencer par

pour arriver a
)
Soit

Calculons

avec

.u=)
.\begin{pmatrix}x\\y\\z\end{pmatrix}=\dfrac{1}{2}\begin{pmatrix}y+z\\-x+z\\-x-y\end{pmatrix}=w\wedge u=\begin{pmatrix}y'z-yz'\\x'z-xz'\\x'y-y'x\end{pmatrix})

je vois pas comment ca va m'aide d'avoir
)
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 24 Jan 2015, 12:50
par jlb » 24 Jan 2015, 12:50
Tu sais qu'il y a une unique solution à ce système: et en observant un peu, il est immédiat que y'=1/2, z'=-1/2 et x'=-1/2 convient et est donc ta solution.
Sinon, tu résous le système d'inconnues x',y',z' comme je te l'ai déjà dit. Sur ce, ce sera ma dernière contribution à ce message et à tes futurs messages.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 24 Jan 2015, 12:58
par jlb » 24 Jan 2015, 12:58
Bon on reprend au début, j'ai mal recopier ton vecteur (-1;1,-1) à la place de (-1;0;1).
Relis tous les messages précédents, je vais les corriger.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 24 Jan 2015, 13:06
par jlb » 24 Jan 2015, 13:06
bah, apprends à calculer!!! la deuxième ligne de ton produit vectoriel est fausse et après comme il y a une solution unique et qu'elle est évidente par identification, je ne vois pas de problèmes particuliers.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 24 Jan 2015, 13:17
par adamNIDO » 24 Jan 2015, 13:17
jlb a écrit:bah, apprends à calculer!!! la deuxième ligne de ton produit vectoriel est fausse et après comme il y a une solution unique et qu'elle est évidente par identification, je ne vois pas de problèmes particuliers.
la deuxième ligne de mon produit vectoriel est vraie, vous êtes incapable de vous expliquer ni latex ni.. que de petit mots sert a rien merci monsieur comme même, mais oubliez que j'ai demande votre aide...
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 24 Jan 2015, 14:00
par jlb » 24 Jan 2015, 14:00
adamNIDO a écrit:
je vois pas comment ca va m'aide d'avoir
)
1° je répète, tu as une erreur dans la ligne x'z-xz' c'est z'x-x'z
2° "je vois pas comment..." "vous êtes incapable..."il n'y a pas que toi qui peut-être susceptible et très désagréable !! mais bon, tu as commencé...depuis longtemps ( j'ai un très bon souvenir de tes réponses sur exo sup...où j'ai eu droit à un " attention à ce que vous écrivez")
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités




appaetient au noyau de A! Donc l'égalité est fausse, car le noyau de A est de dimension 1! Je ne comprends pas tout!!
désigne l'application linéaire
; d'une manière générale, f(.) est une autre notation pour la fonction f.
alors matrice dans la base C de f associe a A est =
pour arriver a
avec
