Matrice et fonction affine

[youkef-sne]

Salut, j'ai un probleme sur un exercice que je ne comprend pas, j'ecris le sujet:

1)Soit A(Xa, Ya) et B(Xb,Yb) deux points de R^2. On note D la droite affine passang par A et par B. Soit M(X, Y) un point de R^2. En exprimant la condition M appartient à D avec un déterminant, donner une équation cartésienne de D.

Je dis que: y=ax+b, avec a= (Yb-Ya)/(Xb-Xa).
Mais pour b je sais pas, et j'sais meme pas si c'esy juste.


2) Soit A(Xa, Ya, Za), B(Xb, Yb, Zb), C(Xc, Yc, Zc) et soit M(X, Y, Z). Tous appartiennent a R^3. On suppose AB et AC non colinéaire, et on note P le plan affine passant par A, B, C. Exprimer la condition M appartient à P avec un determinant et donner une equation cartesienne de P.

3)

[youkef-sne]

Pour b j'ai trouvé de la premiere question j'ai trouvé: (X2Y1-X1Y2)/(X2-X1).

[Pseuda]

Bonsoir,

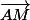M ssi et 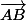sont colinéaires, ce que tu peux exprimer à l'aide d'un déterminant.