Loi du couple (X,X)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Gurvan44
- Membre Naturel
- Messages: 64
- Enregistré le: 20 Juin 2017, 23:25
- Localisation: Nantes (Bouguenais)
-
 par Gurvan44 » 19 Fév 2024, 13:25
par Gurvan44 » 19 Fév 2024, 13:25
Bonjour, je souhaite déterminer la densité jointe du couple
$)
où
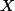
est une v.a. réelle à densité par rapport à Lebesgue

.
Je sais bien faire lorsque je cherche pour
)
avec

et Y indépendant de X, mais là X n'étant pas indépendant de lui-même je bloque un peu.
Mon problème initial est un peu plus général mais j'ai l'impression que le point clé est celui expliqué ci dessus.
Voici le problème général si vous souhaitez :
https://photos.app.goo.gl/47p7x2KjqtNdUcdKAMerci beaucoup pour votre attention, en espérant que qq aura envie de m'aider


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Fév 2024, 15:01
par Ben314 » 19 Fév 2024, 15:01
Salut,
Si tu espère avoir un truc du style
\!\in\!E\big)\!=\!\int\!\int_Ef(x,y)\,dxdy)
, pour une certaine fonction

alors c'est bien évidement foutu d'avance vu que le couple
)
ne prend ses valeurs que sur un ensemble de mesure de Lebesgue nul (à savoir la bissectrice
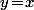
).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Gurvan44
- Membre Naturel
- Messages: 64
- Enregistré le: 20 Juin 2017, 23:25
- Localisation: Nantes (Bouguenais)
-
 par Gurvan44 » 19 Fév 2024, 17:23
par Gurvan44 » 19 Fév 2024, 17:23
Mhh oui en effet, mais du coup par exemple pour la fonction

ci-dessous, est-il possible d'exprimer la densité de

par rapport à Lebesgue sur

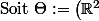^{2}$. Pour $\theta=(a, b) \in \Theta$ \text{, on definit } $g_{\theta}:[0,1] \rightarrow \mathbb{R}^{2}$ par)
=z a+(1-z) b<br />$$)
On note
$)
où


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Fév 2024, 17:36
par Ben314 » 19 Fév 2024, 17:36
Ben non, c'est exactement la même chose : les valeurs prises par
)
c'est le segment

qui a une mesure de Lebesgue (de dimension 2) nulle donc tu ne va pas exprimer ta loi à l'aide de cette mesure.
Par contre, si tu muni le segment

d'une mesure (de dimension 1) induite par ta bijection de [0,1] sur ce segment, là, oui, ta loi s'exprime bien évidement à l'aide de cette mesure, mais ça n'apporte rien vu que c'est exactement la même chose que la définition qu'on te donne . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Gurvan44
- Membre Naturel
- Messages: 64
- Enregistré le: 20 Juin 2017, 23:25
- Localisation: Nantes (Bouguenais)
-
 par Gurvan44 » 20 Fév 2024, 15:25
par Gurvan44 » 20 Fév 2024, 15:25
Ok, du coup si je dois calculer
, A \in \mathbb{R}^2)
, j'ai l'intuition que la réponse sera :
}{\lvert b - a \rvert})
où

est la mesure de Lebesgue sur

.
Mais, si c'est bien ça, comment le justifier un peu mieux ? genre comment démontrer un peu ça ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Fév 2024, 15:34
par Ben314 » 20 Fév 2024, 15:34
je ne pense pas qu'il soit sain d'écrire
)
sans mettre un truc du style

pour bien préciser qu'il s'agit de la mesure de Lesbegue 1-dimensionnelle sur le segment [a,b] du plan.
Et sinon, à mon avis, l’expression de loin la plus simple de
)
c'est celle directement donnée par l'énoncé, à savoir
=\lambda\big(g_{\theta}^{-1}(A)\big))
où là,

désigne bien la "vraie" mesure de Lebesgue sur

.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Gurvan44
- Membre Naturel
- Messages: 64
- Enregistré le: 20 Juin 2017, 23:25
- Localisation: Nantes (Bouguenais)
-
 par Gurvan44 » 28 Fév 2024, 10:44
par Gurvan44 » 28 Fév 2024, 10:44
Yes merci Ben, ça m''a fait de bons rappels ! Bonne journée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
