Limites et factorielles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 10 Jan 2007, 19:52
par humpf » 10 Jan 2007, 19:52
Encore les factorielles...
Cette fois, je dois calculer

.
C'est la limite quand n tend vers l'infini de n factoriel sur n puissance n-1 factoriel.
Mon problème c'est que je ne sais pas du tout comment calculer avec les factorielles... :triste:
Est-ce que quelqu'un peut m'aider?
Merci
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 10 Jan 2007, 19:54
par fahr451 » 10 Jan 2007, 19:54
à ton avis quel est le terme le plus gros entre numérateur et dénominateur ?
de peu de beaucoup?
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 10 Jan 2007, 20:01
par humpf » 10 Jan 2007, 20:01
C'est le dénominateur et de beaucoup. Donc la limite tend vers 0. Donc, si on a utilisé cette limite pour calculer le rayon de convergence, on obtient
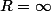
.
C'est juste ou c'est à côté de la plaque?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 10 Jan 2007, 20:05
par fahr451 » 10 Jan 2007, 20:05
pour l instant je ne vois pas de série entière
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 10 Jan 2007, 20:20
par humpf » 10 Jan 2007, 20:20
La série entière c'est :
^n}{n^{n!}} x^n)
Alors, c'est juste ou j'ai encore fait tout faux ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 10 Jan 2007, 20:23
par fahr451 » 10 Jan 2007, 20:23
tu as une série entière sigma des an x^n
et tu viens de "montrer" que an tendait vers 0 tu n 'en déduis surtout pas que R = infini tout ce que tu peut déduire c'est que R>=1
utilise donc là encore le critère de d alembert.
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 10 Jan 2007, 20:26
par humpf » 10 Jan 2007, 20:26
Oups :doh: . Mais on a vu au cours que si la limite L existe alors

.
Et avec d'Alembert, je vois pas comment on fait pour le

?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 10 Jan 2007, 20:30
par Joker62 » 10 Jan 2007, 20:30
Dans ton cours c'est la limite de |a(n+1)/a(n)|
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 10 Jan 2007, 20:31
par Joker62 » 10 Jan 2007, 20:31
Ou apparemment le critère de cauchy avec la racine n-ième que tu as utilisés ici apparemment
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 10 Jan 2007, 20:33
par humpf » 10 Jan 2007, 20:33
Oui, ou bien

.
J'ai pris celle-là. Mais c'est bien possible que je me sois trompée dans les calculs. L'analyse c'est vraiment pas mon point fort :hum:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 10 Jan 2007, 20:35
par Joker62 » 10 Jan 2007, 20:35
Non si c'est bon
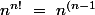!^n})
Tu prends la racine n-ième, la limite tends vers 0, le critère de Cauchy nous affirme que R = 1/0 = +oo par convention
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 10 Jan 2007, 20:38
par humpf » 10 Jan 2007, 20:38
oui, c'était mon raisonnement. Donc c'est bien +

Merci beaucoup pour votre aide!
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Jan 2007, 21:17
par yos » 10 Jan 2007, 21:17
Je comprends rien. Les suites changent sans arrêt. Non aux énoncés instables!
Si je reprends

, on a

donc

, donc
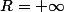
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
