On cherche :
^n x^{n+1}}{n+1}) 1er cas :
1er cas : 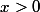
alors
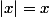
Si
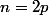
:
^n x^{n+1}}{n+1} = \dfrac{ |x|^{2p +1}}{2p+1} = \dfrac{\exp ((2p+1) \ln|x|)}{2p+1} \longrightarrow + \infty)
par croissances comparées car
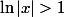
Donc la suite diverge vers

si n est pair.
Si
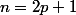
:
^n x^{n+1}}{n+1} =- \dfrac{ |x|^{2p + 2}}{2p+2} =- \dfrac{\exp ((2p+2) \ln|x|)}{2p+2} \longrightarrow - \infty)
par croissances comparées car
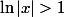
Donc la suite diverge vers

si n est impair.
2ème cas : 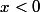
alors
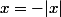
Si
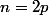
:
^n x^{n+1}}{n+1} = - \dfrac{ |x|^{2p +1}}{2p+1} = - \dfrac{\exp ((2p+1) \ln|x|)}{2p+1} \longrightarrow - \infty)
par croissances comparées car
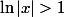
Donc la suite diverge vers

si n est pair.
Si
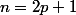
:
^n x^{n+1}}{n+1} =\dfrac{ |x|^{2p + 2}}{2p+2} = \dfrac{\exp ((2p+2) \ln|x|)}{2p+2} \longrightarrow + \infty)
par croissances comparées car
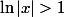
Donc la suite diverge vers

si n est impair.
Les sous suites
)
et
)
ne tendent pas vers la même limite.
Conclusion : la suite n'admet pas de limite (finie ou infinie)