Limite sup inf
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
par kurenay » 31 Oct 2019, 03:02
Bonsoir,
On considère une espace probabilisé
)
et une suite d'événements
_{n \geq 0})
On définit également les ensembles suivants:
1) Montrer que 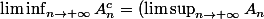^c)
2) Montrer que 
3) Montrer que 
est infinie
4) Montrer que  \leq \liminf_{n \rightarrow \infty} \mathbb{P}(A_n) \leq \limsup_{n \rightarrow \infty} \mathbb{P}(A_n) \leq \mathbb{P}(\limsup_{n \rightarrow \infty} A_n))
1)
^c \Leftrightarrow [\forall i \geq 0, \exists j \geq i, x\in A_j]^c \Leftrightarrow x\in (\bigcup_{i \geq 0} \bigcap_{j \geq i}{A_j}^c))
2)C'est juste la définition d'appartenir l'union puis à l'intersection d'un ensemble, je ne vois pas ce qu'il faut montrer.
3)
ce qui équivaut à dire que x appartient à
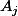
pour un nombre infini de j. (Est-ce suffisant ? )
4)On pose
alors
_n)
est une suite croissante de
et on sait que
= \lim_n \mathbb{P}(B_n))
.
De plus, pour tout
d'où
 \leq inf_{k \geq n} \mathbb{P}(A_k))
et
 \leq \lim_{n \rightarrow \infty}(\inf_{k \geq n} \mathbb{P}(A_k))= \liminf_{n \rightarrow \infty}\mathbb{P}(A_n))
. Après je bloque.
Merci
-
GaBuZoMeu
- Habitué(e)
- Messages: 6120
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 31 Oct 2019, 06:01
Le raisonnement pour la dernière inégalité est tout à fait analogue à celui que tu viens de faire, en renversant l'ordre et le sens des inclusions.
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
par kurenay » 31 Oct 2019, 23:39
Ok je vois c'est bon, la condition
< \infty)
est toujours vrai car c'est une mesure finie.
alors
_n)
est une suite décroissante de
et
donc
= \lim_n \mathbb{P}(B_n))
.
De plus, pour tout
d'où
 \geq sup_{k \geq n} \mathbb{P}(A_k))
et
 \geq \lim_{n \rightarrow \infty}(\sup_{k \geq n} \mathbb{P}(A_k))= \limsup_{n \rightarrow \infty}\mathbb{P}(A_n))
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
par kurenay » 01 Nov 2019, 04:45
5)On admet que  < + \infty)
.
Montrer que 
presque surement.
Ça parait simple mais je n'arrive pas à l'expliquer
 = \lim_{n \rightarrow \infty} \sum_{p=0}^n 1_{A_p}(x))
Le cas ou les
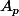
sont 2 à 2 disjoints est vrai car la limite sera égale soit à 0 soit à 1.
Mais pour l'autre cas, j'ai envie de dire que l'hypothèse signifie que x appartient à
que pour un nombre fini de n mais c'est la définition de ce qu'on veut montrer, ça semble trop rapide...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
