Limite sup et inf
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
gorgiel
- Messages: 4
- Enregistré le: 18 Fév 2020, 20:36
-
 par gorgiel » 18 Fév 2020, 20:59
par gorgiel » 18 Fév 2020, 20:59
Bonjour,
Dans mon cours d'analyse , on a définit les limites sup et inf de la façon suivante:
Soit
_{n\in\mathbb{N}}$)
, on pose
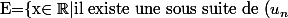_{n\in\mathbb{N}}$ qui converge vers x$\}$)
. Puis, on pose la limite sup de
_{n\in\mathbb{N} })
comme étant le suprémum de E et l'infimum de cet ensemble pour la limite inf.
Mon problème est que je n'arrive pas à calculer ces limites car je n'arrive pas à trouver l'ensemble E.
J'y suis arrivé pour les suites
^n\right),\left(sin(n)\right),\left((-1)^n.\left(1+\frac{1}{n}\right)\right)$)
. Mais pour d'autres suites comme
,\left(\frac{1}{2^n}+\frac{1}{3^n}\right)$)
je bloque.
Quelqu'un pourrait m'expliquer comment trouver cet ensemble E? Puisque à priori trouver le sup et l'inf de cet ensemble ne devrait pas être trop compliqué.
Merci d'avance,
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 18 Fév 2020, 21:06
par GaBuZoMeu » 18 Fév 2020, 21:06
Le cas des suites que tu donnes en exemple est pourtant beaucoup plus simple, puisque ce sont des suites qui convergent.
Quelle peut être la limsup et la liminf d'une suite qui a une limite ?
-
gorgiel
- Messages: 4
- Enregistré le: 18 Fév 2020, 20:36
-
 par gorgiel » 18 Fév 2020, 21:27
par gorgiel » 18 Fév 2020, 21:27
Si je ne me trompe pas, les limsup et liminf vont converger vers la limite de la suite, mais j'aimerais savoir comment calculer ces limites dans le cas où la limite n'existe pas forcément (mais effectivement mes exemples ne sont pas les mieux choisit).
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 18 Fév 2020, 22:25
par GaBuZoMeu » 18 Fév 2020, 22:25
Limsup et liminf ne "convergent" pas, ils sont la limite de la suite quand celle-ci existe.
Après, quand la suite n'est pas convergente, il faut comprendre quelles sont les valeurs d'adhérence d'icelle (je trouve ça joli, "icelle").

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 18 Fév 2020, 23:08
par chombier » 18 Fév 2020, 23:08
gorgiel a écrit:Bonjour,
Dans mon cours d'analyse , on a définit les limites sup et inf de la façon suivante:
Soit
_{n\in\mathbb{N}}$)
, on pose
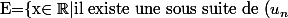_{n\in\mathbb{N}}$ qui converge vers x$\}$)
. Puis, on pose la limite sup de
_{n\in\mathbb{N} })
comme étant le suprémum de E et l'infimum de cet ensemble pour la limite inf.
Mon problème est que je n'arrive pas à calculer ces limites car je n'arrive pas à trouver l'ensemble E.
J'y suis arrivé pour les suites
^n\right),\left(sin(n)\right),\left((-1)^n.\left(1+\frac{1}{n}\right)\right)$)
. Mais pour d'autres suites comme
,\left(\frac{1}{2^n}+\frac{1}{3^n}\right)$)
je bloque.
Quelqu'un pourrait m'expliquer comment trouver cet ensemble E? Puisque à priori trouver le sup et l'inf de cet ensemble ne devrait pas être trop compliqué.
Merci d'avance,
Si on a une suite
_{n \in \mathbb{N})
à valeurs dans

, l'ensemble des réels qui sont limie d'une sous-suite de
_{n \in \mathbb{N})
est confondu avec l'ensemble des valeurs d'adhérences de la suite :
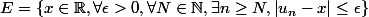
Autrement dit, quel que soit l'intervalle ]

[ considéré, la suite y passe une infinité de fois (dans mon esprit je pense la à comète de Halley, elle finira toujours par repasser à proximité)
Avec ça on voit que la suite est convergente de limite

, alors

, et donc que la limsup et la liminf ce cette sont identiques et égales à

.
Modifié en dernier par
chombier le 19 Fév 2020, 10:04, modifié 4 fois.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 19 Fév 2020, 09:45
par GaBuZoMeu » 19 Fév 2020, 09:45
Chombier, ta définition de valeur d'adhérence n'est pas correcte.

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 19 Fév 2020, 10:04
par chombier » 19 Fév 2020, 10:04
Merci ! J'ai corrigé
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
