Limite sup et inf

[Ncdk]

Bonjour,

J'ai un début d'exercice mais je comprends pas comment ça fonctionne, j'ai besoin d'un petit éclaircissement !

On me donne au début de cette exercice ça :

Soit une suite de parties de . On pose :

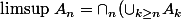et

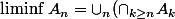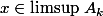
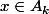
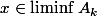
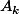
On remarque que si et seulement si pour une infinité d'indices et que si et seulement si appartient à tous les sauf peut-être un nombre fini.

Ma question est que je comprends pas comment fonctionne ce qu'il y a au-dessus...
Si vous pouviez me donner des exemples qui peuvent me faire travailler ces petites formules, ça serait sympa

[zygomatique]

salut

si x appartient à une infinité de A_k alors pour tout n il y a un k > n tel que x est dedans ....

[Ncdk]

D'accord merci

Et concernant les formules, par exemple voir comment ça marche, je sais pas ce que donne :doh:

[zygomatique]

mais ça ne veut rien dire !!!

dans limsup A_n il y a lim ...

[Ncdk]

En effet, merci de tes réponses

[Ncdk]

Du coup j'ai quand même du mal à manipuler cette définition.

On me demande de prouver quelques trucs, mais je sais pas me servir de l'outil qu'on me donne, j'ai certainement pas assez de recul pour comprendre la notion selon moi.

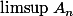
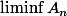
Je dois déterminer la et dans les cas suivants (Avec un ensemble et une suite de parties) :
- est monotone (Croissance et décroissance pour l'inclusion)
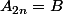
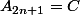
- et où et sont deux parties de
- Les sont deux à deux disjoints

[MouLou]

Du coup j'ai quand même du mal à manipuler cette définition.

On me demande de prouver quelques trucs, mais je sais pas me servir de l'outil qu'on me donne, j'ai certainement pas assez de recul pour comprendre la notion selon moi.

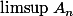
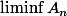
Je dois déterminer la et dans les cas suivants (Avec un ensemble et une suite de parties) :
- est monotone (Croissance et décroissance pour l'inclusion)
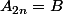
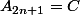
- et où et sont deux parties de
- Les sont deux à deux disjoints

Salut. Par exemple on va prendre An croissante au sens de l inclusion. Tu cherches alors pour la limsup les a qui sont dans une infinité de An. Si tu prends a dans un A_n0, alors par définition d l inclusion il sera dans les An, n>n0. Donc? Cela te donne une première inclusion d un ensemble que je te laisse déterminer dans la limsup. L autre inclusion est immediate. Pour liminf c est très similaire

[Ncdk]

Bonsoir,

Si je suis bien que c'est notre a est dans une infinité de grâce à la croissance pour l'inclusion.
Du coup ?

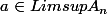
[MouLou]

Bonsoir,

Si je suis bien que c'est notre a est dans une infinité de grâce à la croissance pour l'inclusion.
Du coup ?

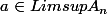
Oui c est ça. En fait il est même dans tous les A_n sauf pour un nombre fini. Tu as donc un exemple ou la limsup est égalé à la liminf

[Ncdk]

Oui c est ça. En fait il est même dans tous les A_n sauf pour un nombre fini. Tu as donc un exemple ou la limsup est égalé à la liminf

Ah oui en effet, mais du coup, pour la décroissance .
Comment je peux m'y prendre ?

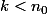
EDIT : Il est dans tous les sauf pour un nombre fini, c'est qu'en fait il faut prendre un et ça il y en a un nombre fini, ce qui conclu que la liminf est la même que la limsup ?