Bonjour,
J'ai un exercice avec une limite de suite, j'ai réussi à l'encadrer sans problème, et j'ai déterminé la limite ainsi en trouvant la limite du majorant, sauf que je n'arrive pas à calculer le minorant, qui, je l'ai vérifié sur Maple, tend bien vers ½ tout comme le majorant. La suite tendant donc vers exp(½) ayant encadré ln(Un) !
Voici la somme en question : sum(k^2/(2*n^4), k = 1 .. n) , j'ai bien sûr le résultat avec Maple mais là n'est pas ce que je recherche, comment est-il possible de calculer une telle somme "à la main" ?
Merci !
Limite de suite (somme de k=1..n)
4 messages
- Page 1 sur 1
Archibald a écrit:Bonsoir,
il y a déjà un membre qui ne dépend pas de l'indice de sommation. Reste ensuite à faire la somme des n premiers carrés.
Bien sûr c'est tout bête ..Je me suis embrouillé entre les n et k Merci ! Et je trouve bien une limite d'½ que ce soit pour le majorant et le minorant donc c'est bon ! :zen:
Bonjour
Tu veux calculer la somme , le calcul est effectivement faisable. La méthode que je vais te proposer se généralise pour le calcul des sommes
, le calcul est effectivement faisable. La méthode que je vais te proposer se généralise pour le calcul des sommes  où p est un entier
où p est un entier  .
.
On pose= \sum_{k=1}^n k^p) , alors
, alors ) et le problème revient à calculer
et le problème revient à calculer ) .
.
On a pour pour k entier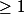 :
: ^3=k^3+3k^2+3k+1) d'où
d'où ^3-k^3=3k^2+3k+1) .
.
En sommant les dernières égalités pour k variant de 1 à n, membres à membres, on obtient:
^3-k^3)=(n+1)^3-1=\sum_{k=1}^n (3k^2++3k+1))
+3S_1(n))
A toi de continuer pour trouver l'expression de) puis celle de S et conclure .
puis celle de S et conclure .
PS. Pour le calculs de) , démarrer de
, démarrer de ^p) pour obtenir l'expression de
pour obtenir l'expression de ^p-k^p) , sommer les égalités pour k variant de 1 à n,..........
, sommer les égalités pour k variant de 1 à n,..........
Baptbe a écrit:Bonjour,
J'ai un exercice avec une limite de suite, j'ai réussi à l'encadrer sans problème, et j'ai déterminé la limite ainsi en trouvant la limite du majorant, sauf que je n'arrive pas à calculer le minorant, qui, je l'ai vérifié sur Maple, tend bien vers ½ tout comme le majorant. La suite tendant donc vers exp(½) ayant encadré ln(Un) !
Voici la somme en question : sum(k^2/(2*n^4), k = 1 .. n) , j'ai bien sûr le résultat avec Maple mais là n'est pas ce que je recherche, comment est-il possible de calculer une telle somme "à la main" ?
Merci !
Tu veux calculer la somme
On pose
On a pour pour k entier
En sommant les dernières égalités pour k variant de 1 à n, membres à membres, on obtient:
A toi de continuer pour trouver l'expression de
PS. Pour le calculs de
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
