Limite somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ZetaH
- Messages: 3
- Enregistré le: 15 Déc 2013, 11:57
-
 par ZetaH » 15 Déc 2013, 12:01
par ZetaH » 15 Déc 2013, 12:01
Bonjour à tous,
je planche sur un exercice mais à vrai dire je suis assez perdu.
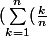^n))
Je me suis dit que découper la somme en deux paquets à l fixé comme ça dans la première somme je peu passer à la limite mais je bute.
Merci d'avance.
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
 par lionel52 » 15 Déc 2013, 13:23
par lionel52 » 15 Déc 2013, 13:23
Bonjour
Si a1,...an sont positifs
(a1+a2+...+an)^n = a1^n + a2^n + ... + an^n + QUELQUE CHOSE DE POSITIF
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 15 Déc 2013, 13:28
par Sourire_banane » 15 Déc 2013, 13:28
Salut,
lionel52 a écrit:Bonjour
Si a1,...an sont positifs
(a1+a2+...+an)^n = a1^n + a2^n + ... + an^n + QUELQUE CHOSE DE POSITIF
???
Il suffit de dire que a1+...+an est positif pour écrire que sa puissance n-ième est positive. Par contre ce que tu prétends est faux.
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 15 Déc 2013, 13:31
par Sourire_banane » 15 Déc 2013, 13:31
Yo,
Est-ce qu'on peut connaitre le libellé de l'exo ?
-
ZetaH
- Messages: 3
- Enregistré le: 15 Déc 2013, 11:57
-
 par ZetaH » 15 Déc 2013, 14:47
par ZetaH » 15 Déc 2013, 14:47
Bonjour, pardonnez cette ineptie, le libellé c'est calculer la limite de la somme quand n tend vers +infini.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 16 Déc 2013, 09:57
par arnaud32 » 16 Déc 2013, 09:57
utilises une comparaison serie integrale
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 16 Déc 2013, 10:13
par nodjim » 16 Déc 2013, 10:13
(1/n)^n est en facteur commun, non ?
ça semble assez trivial.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 16 Déc 2013, 16:24
par arnaud32 » 16 Déc 2013, 16:24
ca doit converger vers

-
ZetaH
- Messages: 3
- Enregistré le: 15 Déc 2013, 11:57
-
 par ZetaH » 16 Déc 2013, 22:49
par ZetaH » 16 Déc 2013, 22:49
Bonjour j'ai réussi l'exercice, mais ce n'est pas trivial j'ai introduit une série de fonctions et utiliser le théorème t'interversion limite et somme.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités