Limite dur à calculer !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Sep 2007, 02:11
par barbu23 » 12 Sep 2007, 02:11
Bonsoir :
Calculer la quantité suivante sans utiliser de DL :
-\frac{\pi}{2}) $)
J'ai utilisé tous les moyens mais j'ai rien trouvé !!
Merci d'avance !!
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 12 Sep 2007, 02:53
par abcd22 » 12 Sep 2007, 02:53
Bonjour,
Si on fait un changement de variable y= 1/x on se retrouve avec quelque chose de la forme
-f(0)}{y-0})
, ça devrait te raappeler quelque chose...
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Sep 2007, 16:44
par barbu23 » 13 Sep 2007, 16:44
D'accord :
On fait un changement de variable :
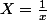

-\frac{\pi}{2}) = \displaystyle \lim_{X \longrightarrow 0} \frac{\arctan(e^{\frac{1}{X}})-\frac{\pi}{2}}{X} $)
Oui, mais là je bloque parceque
 = (\arctan) o (e^{x}) o (\frac{1}{x}) $)
est une fonction composée,donc il faut essayer de composer
-\frac{\pi}{2}}{X} $)
en

produits comme ça :
-\frac{\pi}{2}}{X} = \displaystyle \lim_{X \longrightarrow 0} \frac{\arctan(e^{\frac{1}{X}})-\arctan(e^{\frac{1}{0^{+}}})}{e^{\frac{1}{X}}-e^{\frac{1}{0^{+}}}} \times \frac{e^{\frac{1}{X}}-e^{\frac{1}{0^{+}}}}{\frac{1}{X}-\frac{1}{0^{+}}} \times \frac{\frac{1}{X}-\frac{1}{0^{+}}}{X-0^{+}} = \displaystyle \lim_{X \longrightarrow 0} \frac{\arctan(e^{\frac{1}{X}})-\arctan(e^{\frac{1}{0^{+}}})}{e^{\frac{1}{X}}-e^{\frac{1}{0^{+}}}} \times \displaystyle \lim_{X \longrightarrow 0} \frac{e^{\frac{1}{X}}-e^{\frac{1}{0^{+}}}}{\frac{1}{X}-\frac{1}{0^{+}}} \times \displaystyle \lim_{X \longrightarrow 0} \frac{\frac{1}{X}-\frac{1}{0^{+}}}{X-0^{+}} $)
Est ce que c'est comme ça qu'il faut raisonner !!?
Merci d'avance !!
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 13 Sep 2007, 17:25
par fahr451 » 13 Sep 2007, 17:25
bonjour
j'aurais tendance à dire
arctan y + actan 1/y = pi /2 pour y >0
donc f(x) = - x arctan exp (-x)
et là si on utilise uniquement ( ona le droit ?) arctan u équivalent à u en 0
on obtient f équivalent à - x exp(-x) qui tend vers 0
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 13 Sep 2007, 17:27
par yos » 13 Sep 2007, 17:27
Bof. Je te propose ça :
-\frac{\pi}{2})=\ln u(\arctan u-\frac{\pi}{2})=\ln u(-\arctan\frac{1}{u})=\arctan t\ln t)
et

, donc tout tend vers 0.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Sep 2007, 17:28
par barbu23 » 13 Sep 2007, 17:28
Oui c'est ça c'est la bonne methode !!
merci beaucoup "fahr"
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 13 Sep 2007, 17:28
par yos » 13 Sep 2007, 17:28
Grillé par Fahr!
fahr451 a écrit:et là si on utilise uniquement ( ona le droit ?) arctan u équivalent à u en 0
Je pense : c'est la dérivabilité en 0 de arctan.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Sep 2007, 17:29
par barbu23 » 13 Sep 2007, 17:29
merci à toi aussi yos pour tes eclaircissements !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Sep 2007, 18:51
par barbu23 » 13 Sep 2007, 18:51
"fahr451" :
 $)
~

au voisinage de

.
Après tu dis que :
 $)
~

au voisinage de

.
Mais on n'a pas toujours :

~

~

... Comment tu sais que c'est correcte ?!
Merci d'avance !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Sep 2007, 18:56
par barbu23 » 13 Sep 2007, 18:56
Tu calcules
}{e^{-x}} = 1 $)
puis tu deduis que :
 $)
~

... ??
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 13 Sep 2007, 18:58
par fahr451 » 13 Sep 2007, 18:58
je dis
lim (arctan u) / u = 1 quand u ->0 or
quand x->+infini exp (-x) -> 0 et je compose les limites
lim (arctan (exp(-x) ) / exp (-x) = 1 qd x->+infini
d'une façon générale
si f (x) équivaut à g(x) qd x-> x0
et lim h(t) = x0 qd t ->t0 alors
f (h(t) ) équivaut à g (h(t) ) qd t->t0
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités