Limite-Continuite definitions

[carpe2]

Bonjour à tous,

Je bloque sur un cas particulier.

Rappel definition limite de f en a :
f (fonction) definie sur I, a ;) à I ou ses extrémités.
;) L ;) R, pour tout ;)>0, ;) n>0, pour tout x ;) ]a-n; a+n[ ;) I, |f(x)-L|< ;)

De plus, une propriété me dit : Si f amet une limite L en a et a;)I alors f(a)=L

Ma question est donc la suivante : Comment cette définition de la limite prend-t-elle en compte les cas particuliers de fonctions non continues ? Avec une telle définition de la limite, la fonction f est nécessairement continue, non ?

Ex:
. .I ;) R
f: x ;) f(x) si x;)a
. . . . . . 0 si x=a (dans le cas général ou lim f(x);)0 )
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x;)a
D'après la définition de la limite, cette fonction est impossible.

Je ne sais pas si mes explications sont suffisamment claires. N'h'ésitez pas à me demander des précisions.

Cordialement

[Monsieur23]

Aloha,

Prend le cas plus simple de la fonction qui vaut 0 partout, sauf f(0)=1.

Est-ce que cette fonction à une limite en 0?

[carpe2]

Maintenant que vous posez la question, je commence a douter... x)

La fonction f admet 0 pour limite par valeurs strictement inferieures à 0 et par valeurs strictement supérieures à 0.
Or si on s'en tient à la définition, on ne peux pas dire que f admettent une limite en 0 car pour x=0,
;) ;)>0, tel que |f(0)-0|< ;). Donc ma réponse est non.

[carpe2]

Si j'ai bien saisi ce que vous vouliez mettre en évidence, il ne faut pas confondre f admet une limite en 0 et f admet une limite en 0 par valeurs strictement supérieures et inférieures.

Mais alors, la définition de la limite en un point n'est valable que pour des intervalles sur lesquelles notre fonction est continue ? On ne peux pas parler de limite en 0 pour la fonction f que vous avez précédemment décrite ?

[Mikihisa]

Tout les intervalles ]-n;+n[ avec n>0 contiennent 0.

Basiquement je dirait que si f admet une limite fini en a€I alors f est continue en a, donc si f n'est pas continue en a elle n'a pas de limite en a.

[zygomatique]

salut

pas clair du tout ...

maintenant en reprenant ta définition et l'exemple de Monsieur23 ::

f admet une limite 0 qui est 0 ...... point

maintenant f(0) <> 0 donc f n'est pas continue en 0 .... point

[carpe2]

Oui mais justement, peux-t-on dire que f admet une limite en 0 alors que f(0)=1 ? cela contredit la definition, car ;) ;)>0, tel que |f(0)-0|< ;), non ?

On peux seulement dire qu'elle admet une limite par valeurs strictement sup et inf mais pas en 0, non ?

[Monsieur23]

La fonction que j'ai donnée n'admet pas de limite en 0 ; sinon cette limite serait f(0)=1, et ce n'est pas possible.

On peut dire que la fonction restreinte à R+* (ou R-*) a une limite en 0, qui est 0 ;-)

[arnaud32]

c'est la notion de limite epointee
http://fr.wikipedia.org/wiki/Limite_(math%C3%A9matiques)

[Mikihisa]

f n'as pas de limite en 0.

Comme je l'ai dit, si f admet une limite finie en a€I alors f est continue, et la limite vaut necessairement f(a).

Donc limite fini en a => continue, et pas de limite ou limite infinie => pas continue ( car la propriété est en fait une CNS).

[deltab]

Bonjour.

c'est la notion de limite epointee
http://fr.wikipedia.org/wiki/Limite_(math%C3%A9matiques)

Ton lien ne donne rien, voir plutôt celui-la
Erreur sur le lien la parenthèse finale écrite doit faire partie du lien, elle est écrite en noir et non en bleu).

[deltab]

Bonjour.

f n'as pas de limite en 0.

Comme je l'ai dit, si f admet une limite finie en a€I alors f est continue, et la limite vaut necessairement f(a).

Donc limite fini en a => continue, et pas de limite ou limite infinie => pas continue ( car la propriété est en fait une CNS).

La définition que j'ai apprise est celle de limite épointée pour laquelle est continue en si est définie en et 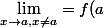(limite au sens limite épointée).
La définition qu'a donnée Carpe2 est une autre définition de la limite non équivalente à la limite épointée pour laquelle la notion de continuité perd son sens, si f est définie en a, alors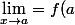 (grâce à l'unité de la limite).

[carpe2]

Merci pour vos réponses :-)
En ce qui me concerne, c'est déjà plus clair :)

[zygomatique]

f est continue en a signifie :: f(a) existe et


g admet une limite en a signifie ::

ceci sous-entend que tendre vers a c'est être aussi proche que l'on veut de a ... sans forcément être a

g est continue en a signifie :: g(a) = r

:lol3:

[Mikihisa]

Zygo : ta définition de la limite n'a aucun sens : en gros tu dis que f a une limite en a si f a une limite en a.

La définition de la limite la plus courante est :

[zygomatique]

relis ce que j'ai écrit ....

[deltab]

Bonjour.

On dit que f tend vers L quand x tend vers a si :
De cette définition, on déduit que si est définie en et admet une limite quand tend vers , alors ce qui n'est pas le cas avec la limite épointée

[Synar]

Je ferais juste noté que beaucoup de quiproquos peuvent venir du fait qu'en France, la notion de limite est souvent définie en licence comme limite épointée (ce qui correspond aussi je crois à la définition étrangère) alors qu'en prépa elle est définie comme limite non-épointée, d'où de nombreuses incompréhensions potentielles. (Par ailleurs, je suis curieux de savoir ce qu'il en est en master ou en école d'ingé, et dans la recherche en général (même si à un tel niveau ça n'a plus trop d'importances).)

[Mikihisa]

Personnellement je n'aime pas cette définition de limite épointé, elle ne fait que compliquer la définition de la continuité. Dans le cas ou il n'y a pas de limite mais qu'il existe une limite épointé on peux toujours changer la valeure de la fonction pour la rendre continue.

Et puis la définition de la limite dans un cadre plus général ne correspond pas a celle de la limite épointée.

Zygo : j'ai très bien lu ce que tu as écrit: tu dis que "g a une limite en a si il existe r tel quel lim g(x)=r", la notation "lim g(x)=r" sous entend que la limite existe, donc en gros tu dis que "g a une limite si g a une limite" ce qui n'a aucun sens.

[deltab]

Bonjour.

Personnellement je n'aime pas cette définition de limite épointé, elle ne fait que compliquer la définition de la continuité. Dans le cas ou il n'y a pas de limite mais qu'il existe une limite épointé on peux toujours changer la valeure de la fonction pour la rendre continue.

Dans les différentes définitions données de la limite, personne n' a jugé nécessaire de préciser la notation moi-même compris.
Ce que tu reproches à Zygo, tu viens toi-même de le faire (abus de langage et de notation)