Les applications el les ensembles

[l3rab]

j'ai pas compris le corigé du cette exercice ci-dessous , est ce que il existe une demonstration plus facile ?
http://www.bibmath.net/ressources/index ... &type=fexo exercice 26
ce que précisément j'ai pas compris dans la question 2 ou on a utilise l'hpothese (f est surjective) et pour quoi on a traité seulment le cas ou X intersection B= ensemble vide ? que ce qu'il passe si on prend un X sous ensemble de E tel que l'image de X et un ensemble non vide * ensemble non vide

[GaBuZoMeu]

On veut montrer que pour tout , on a (et donc ).
Soit . On utilise la surjectivité de pour montrer . Pour cela on choisit , et la surjectivité de implique qu'il existe une parti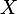e de 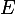telle que , c.-à-d. que et . Ces égalités montrent que et .

[l3rab]

On veut montrer que pour tout , on a (et donc ).
Soit . On utilise la surjectivité de pour montrer . Pour cela on choisit , et la surjectivité de implique qu'il existe une partie de telle que , c.-à-d. que et . Ces égalités montrent que et .

mais monsieur , pour qoui tu choisis ?? pour quoi tu choisis l'ensemble vide ??

[GaBuZoMeu]

Pour le raisonnement, on choisit d'un côté une partie de qui contient : quoi de plus naturel que 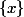? et de l'autre une partie de qui ne contient pas : quoi de plus naturel que ?

Relis calmement et sérieusement le raisonnement, pour bien comprendre comment il marche.