Just for fun : Intégrale convergente

par **Nightmare** » 14 Aoû 2006, 21:59

Bonsoir

Voici un exercice sympathique pour ceux qui s'ennuient :

Soient a et b deux réels quelconques.
Démontrez que l'intégrale impropre suivante est convergente et calculez sa limite :

Bon courage

:happy3:

par **tize** » 14 Aoû 2006, 22:04

Le fonction est prolongeable par continuité en 0 et

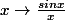
est intégrable sur

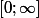
(classique avec une IPP). Après changement de variable, c'est la même chose que :

En remplacant sin(x) par sa serie entiere on trouve

et donc :

Sauf erreur de ma part

par **Nightmare** » 14 Aoû 2006, 22:14

Salut tize.

Oui c'est une solution, mais maintenant supposons que l'on ne connait pas la valeur de

Il y a une méthode qui permet de ne pas avoir à calculer cette dernière intégrale.

:happy3:

par **alben** » 14 Aoû 2006, 22:15

Bonsoir,

Moi je dis zéro

par **tize** » 14 Aoû 2006, 22:16

En remplacant sin(x) par sa serie entiere on trouve

et donc :

Sauf erreur de ma part

par **nekros** » 14 Aoû 2006, 22:19

Bonjour Nightmare,

On note

Un développement limité en 0 donne :

On peut donc prolonger f en 0 en posant

Par linéarité de l'intégrale, on a :

Or,

qui converge lorsque c tend vers l'infini.

Conclusion : l'intégrale converge

Je cherche la limite...

par **tize** » 14 Aoû 2006, 22:19

Nightmare a écrit:Salut tize.

Oui c'est une solution, mais maintenant supposons que l'on ne connait pas la valeur de

Il y a une méthode qui permet de ne pas avoir à calculer cette dernière intégrale.

:happy3:

même avec b=1 et a=0 ?

par **Nightmare** » 14 Aoû 2006, 22:26

Un indice : Utiliser le théorème de fubini

par **Nightmare** » 14 Aoû 2006, 22:27

Hum attendez je vérifie je crois que j'ai fait une belle erreur dans mes calculs :briques:

par **Nightmare** » 14 Aoû 2006, 22:31

Arf oui j'ai fait une terrible erreur ...

En fait j'avais écrit que :

Par conséquent notre intégrale est égale à :

Soit par le théorème de Fubini :

Seulement

n'existe pas ...

par **nekros** » 14 Aoû 2006, 22:34

On peut retrouver ce résultat en calculant l'intégrale double :

avec

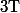
dans

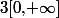
Cependant, c'est assez long.

Thomas G :zen:

par **alben** » 15 Aoû 2006, 00:01

On démontre assez facilement que sin(x)/x est intégrable de 0 à l'infini
donc

par **nekros** » 15 Aoû 2006, 00:05

Bonjour Alben,

Tu as posé u=ax et u=bx :hein:

par **alben** » 15 Aoû 2006, 00:12

Oui, j'aurai pu utiliser u et v, ça ne changeait rien
NB j'ai corrigé une petite erreur sur le 2ième intégrale du à la place de dx

par **Nightmare** » 15 Aoû 2006, 00:27

Comment calcules tu

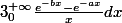
avec cette méthode ?

par **nekros** » 15 Aoû 2006, 00:33

Tiens ça me rappelle quelque chose cette intégrale :lol4:

par **alben** » 15 Aoû 2006, 00:50

nekros a écrit:alben > la deuxième égalité est fausse, ça revient à dire que ax=bx

.
Je ne comprends pas ta remarque. Je peux reformuler ainsi

Les deux variables u et v sont des variables muettes, elles n'interviennenbt pas dans le résultat final qui est identique dans les deux cas.
Nightmare, c'est un piège car l'exponentielle intégrale a un problème au voisinage de zéro.
En choisissant un h petit et et supposant a et b tous deux positifs, je dois pouvoir trouver quelque chose

par **nekros** » 15 Aoû 2006, 00:52

Mais comment expliques-tu le fait que tu ne trouves pas la même limite ?

par **Nightmare** » 15 Aoû 2006, 00:52

Eh oui Nekros :happy3:

Je me suis inspiré de cette intégrale justement pour la mienne !

par **nekros** » 15 Aoû 2006, 00:54

Nightmare a écrit:Eh oui Nekros :happy3:

Je me suis inspiré de cette intégrale justement pour la mienne !

Je m'en doutais :ptdr:

En tout cas, merci pour l'exo !

Just for fun : Intégrale convergente

Just for fun : Intégrale convergente

Qui est en ligne