Intersection
17 messages
- Page 1 sur 1
Intersection
Bonjour,
Un exercice demandait l'intersection des [-1/n,1/n] et ]-1/n,1/n[. Respectivement 0 et ensemble vide (qui se démontre avec limite ou avec double implication). Mais là, question de l'intersection pour les n naturels de l'intervalle [n,+oo[. Aidez-moi svp, ça s'écrit l'intervalle "]+oo,+oo[" ?
Merci d'avance.
Un exercice demandait l'intersection des [-1/n,1/n] et ]-1/n,1/n[. Respectivement 0 et ensemble vide (qui se démontre avec limite ou avec double implication). Mais là, question de l'intersection pour les n naturels de l'intervalle [n,+oo[. Aidez-moi svp, ça s'écrit l'intervalle "]+oo,+oo[" ?
Merci d'avance.
Re: Intersection
Bonjour,
L'intervalle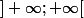 n'a pas de sens (sauf à considérer la droite réelle complétée des infinis).
n'a pas de sens (sauf à considérer la droite réelle complétée des infinis).
Mais votre intuition n'est pas dénuée de sens ; quels sont alors les réels qui appartiendraient à un tel intervalle ?
Pour en revenir à une démarche plus rigoureuse ici : quels sont les réels qui appartiennent à tous les intervalles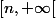 pour
pour 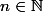 ? Cela définit un ensemble, comment l'appelle-t-on ?
? Cela définit un ensemble, comment l'appelle-t-on ?
L'intervalle
Mais votre intuition n'est pas dénuée de sens ; quels sont alors les réels qui appartiendraient à un tel intervalle ?
Pour en revenir à une démarche plus rigoureuse ici : quels sont les réels qui appartiennent à tous les intervalles
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Intersection
Bonjour,
Pour donner un sens à cet "intervalle" :
Cette intersection contient-elle un réel? (raisonner par l'absurde par exemple)
Conclusion ?
@hdci
Pour donner un sens à cet "intervalle" :
Cette intersection contient-elle un réel? (raisonner par l'absurde par exemple)
Conclusion ?
@hdci
Re: Intersection
Salut,
Ensuite j'aimerais bien voir comment tu démontre que l'intersection des ]-1/n;1/n[ c'est l'ensemble vide.
Enfin, j'aimerais bien que tu m'explique quel raisonnement on ne peut plus biscornu te conduit à penser que, par exemple le réel -5 (qui est dans ]-oo,+oo[) est dans l'intersection des [n,+oo[, c'est a dire que -5 est dans [1,+oo[ ainsi que dans [2,+oo[ ainsi que dans [3,+oo[ ainsi que dans [4,+oo[ etc...
Déjà, l'intersection des [-1/n,1/n], c'est sûrement pas 0 vu qu'une intersection d'ensembles, c'est un ensemble et que 0, c'est pas un ensemble.qaterio a écrit:Un exercice demandait l'intersection des [-1/n,1/n] et ]-1/n,1/n[. Respectivement 0 et ensemble vide (qui se démontre avec limite ou avec double implication). Mais là, question de l'intersection pour les n naturels de l'intervalle [n,+oo[.
Ensuite j'aimerais bien voir comment tu démontre que l'intersection des ]-1/n;1/n[ c'est l'ensemble vide.
Un petit "rappel" : l'intersection d'un certain nombre d'ensembles, c'est les élément qui sont communs à tout ces ensembles : AnBnC c'est les élément qui sont dans A et dans B et dans C.qaterio a écrit:Mais là, question de l'intersection pour les n naturels de l'intervalle [n,+oo[. Aidez-moi svp, ça s'écrit l'intervalle "]+oo,+oo[" ?
Enfin, j'aimerais bien que tu m'explique quel raisonnement on ne peut plus biscornu te conduit à penser que, par exemple le réel -5 (qui est dans ]-oo,+oo[) est dans l'intersection des [n,+oo[, c'est a dire que -5 est dans [1,+oo[ ainsi que dans [2,+oo[ ainsi que dans [3,+oo[ ainsi que dans [4,+oo[ etc...
Modifié en dernier par Ben314 le 19 Sep 2018, 20:03, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intersection
qaterio a écrit:Un exercice demandait l'intersection des [-1/n,1/n] et ]-1/n,1/n[. Respectivement 0 et ensemble vide
Ouh là je n'avais pas vu le début du message... Heureusement Ben314 a bien relevé le point.
@Ben314, qaterio n'a pas écrit
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Intersection
Hdci, oui mais les élements s'éliminent petits à petits comme il s'agit d'une infinité d'intersection.
Ben314,
Alors, pour démontrer [-1/n,1/n] j'ai utilisé une double implication mais comme je ne maîtrise pas trop la manière d'écrire avec ce site je peux dire que [-1/n+1,1/n+1] est strictement inclus dans [-1/n,1/n] et donc cette intersection correspond à la limite quand n tend vers +oo de [-1/n+1,1/n+1] qui vaut [0-,0+], c'est-à-dire {0]. Même raisonnement pour ]-1/n,1/n[ sauf que 0 est exclus, c'est donc l'ensemble vide.
J'ai pas dit que -5 appartenait à cet intervalle. J'ai dit que concrètement, si on devait résoudre cette intersection on obtiendrait [+oo,+oo[, et je demandais si on pouvait réellement écrire ça.
LB2,
Je vais essayer avec l'absurde de suite !
Ben314,
Alors, pour démontrer [-1/n,1/n] j'ai utilisé une double implication mais comme je ne maîtrise pas trop la manière d'écrire avec ce site je peux dire que [-1/n+1,1/n+1] est strictement inclus dans [-1/n,1/n] et donc cette intersection correspond à la limite quand n tend vers +oo de [-1/n+1,1/n+1] qui vaut [0-,0+], c'est-à-dire {0]. Même raisonnement pour ]-1/n,1/n[ sauf que 0 est exclus, c'est donc l'ensemble vide.
J'ai pas dit que -5 appartenait à cet intervalle. J'ai dit que concrètement, si on devait résoudre cette intersection on obtiendrait [+oo,+oo[, et je demandais si on pouvait réellement écrire ça.
LB2,
Je vais essayer avec l'absurde de suite !
Re: Intersection
LB2,
Supposons que ]+oo,+oo[ contienne au moins un élément,
soit n cet élément, on aurait alors n>+oo, ce qui est absurde. On en déduit donc que cet ensemble est l'ensemble vide.
C'est bon ?
Supposons que ]+oo,+oo[ contienne au moins un élément,
soit n cet élément, on aurait alors n>+oo, ce qui est absurde. On en déduit donc que cet ensemble est l'ensemble vide.
C'est bon ?
Re: Intersection
qaterio a écrit:LB2,
Supposons que ]+oo,+oo[ contienne au moins un élément,
soit n cet élément, on aurait alors n>+oo, ce qui est absurde. On en déduit donc que cet ensemble est l'ensemble vide.
C'est bon ?
Oui... et non ; sauf à vous placer "dans l'ensemble des réels complétés des infinis", ce qui suppose pas mal d'autres choses (comme repréciser la relation d'ordre dans cet ensemble), vous ne pouvez pas parler de l'intervalle
Comme vous le dites ici
qaterio a écrit:Hdci, oui mais les élements s'éliminent petits à petits comme il s'agit d'une infinité d'intersection.
c'est là que vous pouvez faire votre raisonnement : appelez
Or
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Intersection
Effectivement, j'avais mal lu.hdci a écrit:@Ben314, qaterio n'a pas écritmais
(d'où les réponses de LB2 et la mienne).
Donc il n'y avait que 1/4 + 1 + 1/2 conneries et pas 1/4 + 1 + 1 comme je l'avais pensé...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intersection
Moi, je veut bien, mais tu peut me dire ce que c'est la définition d'une "limite d'ensembles" ?qaterio a écrit:...cette intersection correspond à la limite quand n tend vers +oo de [-1/n+1,1/n+1] qui vaut [0-,0+], c'est-à-dire {0}.
Et/ou me dire à quelle endroit tu as vu cette définition ?
De même, je connais la définition de [a,b] : c'est les réels x tels que a
Et je connais aussi la définition de
Mais un truc comme ton [a-,b+], ça m’intéresserait plus que beaucoup de voir ce que tu me propose comme définition...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intersection
hdci,
bah oui, vous avez totalement raison, je peux pas me permettre de dire ]+oo,+oo[ c'était même un truc qui m'embêtait dans cette question. C'est même beaucoup plus rigoureux et juste comme ça (on se sert de la définition de l'intervalle. En plus c'est ce que j'avais fait pour le premier: (il existe k réel tel que pour tout entier naturel n non nul, -1/n<=k<=1/n)<=>(k=0) mais là, comme il s'agissait de l'ensemble vide, ça m'embêter, mais ça n'aurait pas dû, j'aurais du penser à utiliser la contraposition pour me sortir du problème)). Ca m'embête de demander de l'aide pour des questions comme ça, mais en même temps, je me posais la question sur la réelle justesse d'une notation ]+oo,+oo[. D'après vos réponses, c'est complètement faux.
En tout cas merci de m'avoir éclairé, je ferai en sorte de me lancer même si j'hésite à mettre une question sous forme d'implications car il ne faut pas oublier que c'est un raisonnement puissant la contraposition !
bah oui, vous avez totalement raison, je peux pas me permettre de dire ]+oo,+oo[ c'était même un truc qui m'embêtait dans cette question. C'est même beaucoup plus rigoureux et juste comme ça (on se sert de la définition de l'intervalle. En plus c'est ce que j'avais fait pour le premier: (il existe k réel tel que pour tout entier naturel n non nul, -1/n<=k<=1/n)<=>(k=0) mais là, comme il s'agissait de l'ensemble vide, ça m'embêter, mais ça n'aurait pas dû, j'aurais du penser à utiliser la contraposition pour me sortir du problème)). Ca m'embête de demander de l'aide pour des questions comme ça, mais en même temps, je me posais la question sur la réelle justesse d'une notation ]+oo,+oo[. D'après vos réponses, c'est complètement faux.
En tout cas merci de m'avoir éclairé, je ferai en sorte de me lancer même si j'hésite à mettre une question sous forme d'implications car il ne faut pas oublier que c'est un raisonnement puissant la contraposition !
Modifié en dernier par qaterio le 19 Sep 2018, 20:20, modifié 1 fois.
Re: Intersection
Ben314,
J'ai pas utiliser la notion de limite pour la démonstration. C'est juste que comme c'est beaucoup trop long à écrire (je ne sais sais me servir des outils sur ce site), j'ai penser à cette manière de faire. On montre que k=0 convient à cet intervalle puiss on montre que k différent de 0 ne convient pas (contraposition) et donc par double implication, on a montré le résultat conjecturé.
J'ai pas utiliser la notion de limite pour la démonstration. C'est juste que comme c'est beaucoup trop long à écrire (je ne sais sais me servir des outils sur ce site), j'ai penser à cette manière de faire. On montre que k=0 convient à cet intervalle puiss on montre que k différent de 0 ne convient pas (contraposition) et donc par double implication, on a montré le résultat conjecturé.
Re: Intersection
Dans ce cas, c'est O.K. et intuitivement parlant, ton truc c'est bien la "limite des ensembles" (sauf que formellement parlant, on a plus que beaucoup du mal à définir proprement ce qu'est une "limite d'ensembles").
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intersection
Ben314,
Vous avez raison, j'ai pensé à ce raisonnement tellement vite que j'avais même pas fais gaffe que cette notion de limite d'intervalles n'était pas bien définie. Mais vous faites bien de me le dire, car en concours, j'aurai été tenter d'utiliser cette "méthode", beaucoup plus rapide ... mais pas valide.
Vous avez raison, j'ai pensé à ce raisonnement tellement vite que j'avais même pas fais gaffe que cette notion de limite d'intervalles n'était pas bien définie. Mais vous faites bien de me le dire, car en concours, j'aurai été tenter d'utiliser cette "méthode", beaucoup plus rapide ... mais pas valide.
Re: Intersection
Ben normalement, même rédigé archi super bien, ça tient tout au plus trois lignes :
- Si un réel est dans l'intersection des
est dans l'intersection des 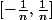 ,
, 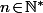 alors, par définition, on a
alors, par définition, on a 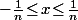 pour tout
pour tout 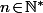 ce qui implique que
ce qui implique que 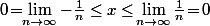 (*) c'est à dire que
(*) c'est à dire que 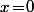 : On a donc
: On a donc 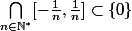
- Réciproquement, si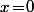 , il est clair que
, il est clair que 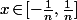 pour tout
pour tout 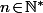 : On a donc
: On a donc 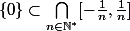
(*) Et si vraiment tu veut "raconter ta vie", tu précise que ça provient directement du théorème (vu en term.) qui dit que, si une suite convergente_{n\in\mathbb N}) est telle que
est telle que 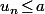 pour tout
pour tout  alors sa limite est elle aussi
alors sa limite est elle aussi 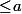 (et idem avec
(et idem avec  à la place de
à la place de  )
)
- Si un réel
- Réciproquement, si
(*) Et si vraiment tu veut "raconter ta vie", tu précise que ça provient directement du théorème (vu en term.) qui dit que, si une suite convergente
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intersection
Du coup elle est valide cette méthode ? parce que dans ma tête c'était comme ça que je pensais. Enfaîte, c'est juste le terme que j'ai employé qui était faux j'imagine, il faut appliquer la limite à la définition de l'intervalle et pas parlé de limite d'intervalle, ok, bah du coup en concours, c'est clairement comme ça que je rédigerais; la démonstration avec l'équivalence m'a pris une page, le calcul est vite fait que ce n'est pas optimisé son temps!
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
