équation de l'intersection de deux disques
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Juil 2009, 16:22
par Pythales » 21 Juil 2009, 16:22
Oui. On part de

et on s'arrête à
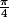
(1ère bissectrice), et on multiplie par 2 à cause de la symétrie.
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 21 Juil 2009, 16:45
par flo22 » 21 Juil 2009, 16:45
OK je pense avoir compris. J'en ai une autre, qui m'a l'air plus compliquée. J'ai bricolé quelque chose sans vraiment être sûr de ce sur quoi je m'appuyais.
Donc je dois intégrer sur
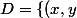 \in \mathbb{R} , x^2+y^2-x \leq 0,x^2+y^2-y\geq 0,y\geq 0\})
Est-ce que j'ai raison de dire que l'aire est décrite par :

D'ailleurs je devrais peut-être plutôt dire

puisque la fonction que j'ai à intégrer n'est pas symétrique
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Juil 2009, 17:01
par Pythales » 21 Juil 2009, 17:01
Tu es sûr que ce n'est pas

?
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 21 Juil 2009, 17:02
par flo22 » 21 Juil 2009, 17:02
Oui pardon je viens de changer
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Juil 2009, 17:08
par Pythales » 21 Juil 2009, 17:08
C'est

-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 21 Juil 2009, 17:15
par flo22 » 21 Juil 2009, 17:15
Et pourquoi ce que j'ai proposé ne vas pas ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Juil 2009, 17:35
par Pythales » 21 Juil 2009, 17:35
Je ne comprends pas pourquoi le

Ce qui aurait été bon est

-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 21 Juil 2009, 17:38
par flo22 » 21 Juil 2009, 17:38
OK je vois. Moi j'ai voulu calculer la moitié de l'aire du disque entier et ensuite retrancher l'intersection avec l'autre disque. Mon calcul est bon si je veux la valeur de l'aire non ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Juil 2009, 17:49
par Pythales » 21 Juil 2009, 17:49
Tu peux vérifier le résultat avec ce qui a été trouvé précédemment, avec

On doit trouver
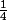
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 21 Juil 2009, 17:51
par flo22 » 21 Juil 2009, 17:51
oui Maple me donne 1/4 pour les deux calculs en ce qui concerne l'aire, et y'a une différence de 10/45 en ce qui concerne la double intégrale que j'ai à calculer.
En fait je vois bien pourquoi ce que tu propose est bon, mais pas vraiment pourquoi ce que moi je propose est faux
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Juil 2009, 18:58
par Pythales » 21 Juil 2009, 18:58
Ce n'est pas

mais

ou encore

-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 21 Juil 2009, 19:01
par flo22 » 21 Juil 2009, 19:01
OK je vois. C'est un hasard que le calcul marche pour l'aire ?
Non puisque je calcule l'aire du même disque mais dont le centre est en (0,1/2), c'est ça ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 22 Juil 2009, 06:49
par Pythales » 22 Juil 2009, 06:49
L'aire du cercle centré en
)
est

Mais pourquoi utiliser une intégrale double pour calculer l'aire d'un demi-cercle !?
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 22 Juil 2009, 11:23
par flo22 » 22 Juil 2009, 11:23
C'est juste pour savoir si je comprends bien...
Mais ce que je n'arrive pas saisir, c'est pourquoi le calcul que j'ai proposé, avec le

nous donne le bon résultat quant à la valeur de l'aire, mais pas le bon en ce qui concerne l'intégrale double, qui au fait est
^2 dx dy)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 22 Juil 2009, 13:55
par Pythales » 22 Juil 2009, 13:55
Décidemment chaque question en appelle une autre ...
Il se trouve que

la 1ère intégrale représentant l'aire du cercle centré sur
)
du fait de la périodicité de
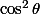
Par contre, en ce qui concerne
^2dxdy)
la fonction
^2)
ne prend pas les mêmes valeurs dans le cercle centré en
)
et dans celui centré en
)
, d'où la différence.
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 22 Juil 2009, 14:06
par flo22 » 22 Juil 2009, 14:06
OK merci, je boucle cet exo (et surtout ce sujet) là dessus ! Merci pour ton aide ! :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
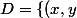 \in \mathbb{R} , x^2+y^2-x \leq 0,x^2+y^2-y\geq 0,y\geq 0\})


 la 1ère intégrale représentant l'aire du cercle centré sur
la 1ère intégrale représentant l'aire du cercle centré sur ) du fait de la périodicité de
du fait de la périodicité de 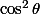
^2dxdy) la fonction
la fonction ^2) ne prend pas les mêmes valeurs dans le cercle centré en
ne prend pas les mêmes valeurs dans le cercle centré en ) et dans celui centré en
et dans celui centré en ) , d'où la différence.
, d'où la différence.