Intersection de sous groupe.

[juve1897]

bj:
non tu as montré que y-1 appartient à l'intersection ..et x appartient aussi à l'intersection et tu as dedui que x*(y-1) apppartient à l'intersection.....( vous avez utilisez le fait que l'intersection est stable !!!!!!!

Merci Charif (tu peux le tutoyer, vu que je me suis permis de le faire, j'espère que ça ne te dérange pas.)

en fait j'utilise la partie 3) que Doraki a redigé ???

En fait les points à verifier sont:


1) element neutre ( )
2) x * y
3) x *

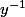
Mais le truc que je ne comprends pas c'est le x * y ???
Il signifie quoi au juste ??? Que l'operation sur X appliquée à l'element x et y ()est encore dans X ???

Par exemple (X,+) notre * est en fait l'opération d'addition
Donc il faut montre que ???

[juve1897]

J'ai fait plein de copié-collés ça va vite.
Le mécanisme derrière chaque petite preuve est le même, c'est ça qui est important.
Et ce genre de preuves t'en as partout, c'est important de pouvoir refaire ça facilement.

Ben oui car les démonstrations sur les sous groupes reposent sur les mm prop
1) element neutre
2) x *

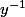
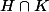
Mais pourquoi on a pas montré que est associatif ???
ça fait partie des point à verifier non ???

[charif]

bj

en faiT la lois * est une application du produit cartésion H*H vers H. donc si on applique la lois à deux élemts on trouve un autre élement z=x*y qui apppartient aussi à H....


REGARDE :

une parite H est un sous groupe de G :

1) H est non vide ET H est inclue dans G

2) SOIT x et y appartient à H ..alors x*(y-1) apppartient à H


ou bien

une partie H est un sous groupe de G :

1) H est non vide ET H est inclue dans G

2) pour x appartient à H ...x-1 appartient à H

3) h est stable par *



ses propositions sont équivalentes

[juve1897]

bj

en faiT la lois * est une application du produit cartésion H*H vers H. donc si on applique la lois à deux élemts on trouve un autre élement z=x*y qui apppartient aussi à H....


REGARDE :

une parite H est un sous groupe de G :

1) H est non vide ET H est inclue dans G

2) SOIT x et y appartient à H ..alors x*(y-1) apppartient à H


ou bien

une partie H est un sous groupe de G :

1) H est non vide ET H est inclue dans G

2) pour x appartient à H ...x-1 appartient à H

3) h est stable par *



ses propositions sont équivalentes

Merci Charif, donc il est plus rapide de montrer par la première méthode (enfin moins long à ecrire quoi).

Mais pourquoi la prop est fausse pour l'union ???

[charif]

bj:


l'exo est un grand classique :soit H et K deux groupes.. HUK est groupe que si H est inclu dans K oubien K est inclu dans H....

[Doraki]

Ben oui car les démonstrations sur les sous groupes reposent sur les mm prop
1) element neutre
2) x *

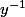
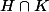
Mais pourquoi on a pas montré que est associatif ???
ça fait partie des point à verifier non ???

J'ai pas tellement compris ton post. Tu m'expliques ce que c'est qu'un ensemble associatif ?

On a montré que X est un sousgroupe de (G,*).
Bien sur, un sous groupe d'un groupe, c'est un groupe (c'est fait pour ça après tout) mais c'est un autre théorème.

Comme c'est la même loi * que dans G, c'est pas très dur de montrer que comme elle est associative dans G, elle reste associative quand on restreint son domaine de définition à X.

[juve1897]

J'ai pas tellement compris ton post. Tu m'expliques ce que c'est qu'un ensemble associatif ?

On a montré que X est un sousgroupe de (G,*).
Bien sur, un sous groupe d'un groupe, c'est un groupe (c'est fait pour ça après tout) mais c'est un autre théorème.

Comme c'est la même loi * que dans G, c'est pas très dur de montrer que comme elle est associative dans G, elle reste associative quand on restreint son domaine de définition à X.

Non, :girl2: c'est vrai que des fois je m'exprime mal.

En fait je te disais qu'il suffisait de montrer que
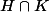
X = on a
1) element neutre
2) x * y-1 appartient à X
pour montrer que c un sous groupe.

Et ensuite je te demandais pourquoi nous n'avons pas montrer en plus que X est associatif ? Car il me semble que c'ets aussi une prop à demontrer pour que X sous un sous groupe.

Mais comme tu me dis que ce n'est pas necessaire je te crois.

J'espere que c'est plus clair :euh: