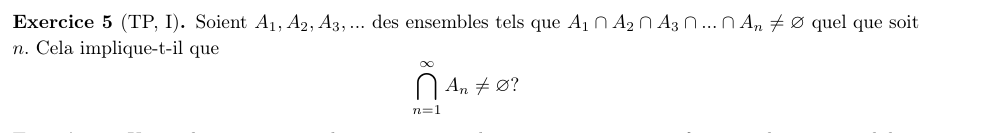
Intersection de familles d'ensembles
7 messages
- Page 1 sur 1
Intersection de familles d'ensembles
Bonjour, j'ai du mal à concevoir pourquoi cette affirmation est fausse et donc à trouver un contre exemple help 
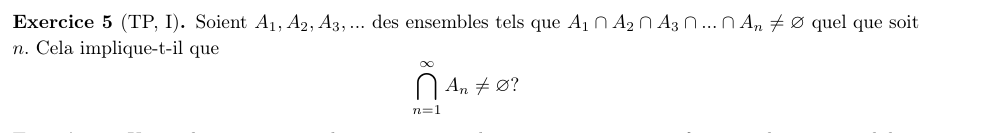
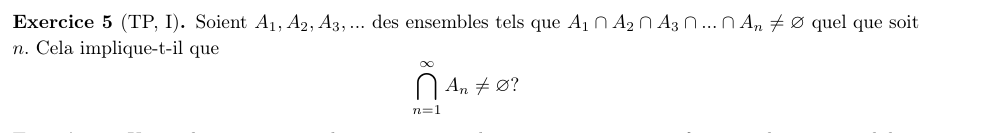
Re: Intersection de familles d'ensembles
Bonjour
Pour tout k entier , k > 0 :
Ak = ] 0 , 1/k ]
OK pour vous ?
Pour tout k entier , k > 0 :
Ak = ] 0 , 1/k ]
OK pour vous ?
Re: Intersection de familles d'ensembles
Salut,
Autre exemple : An = l'ensemble des entiers naturels multiple de n.
On peut aussi noter que si non seulement les intersections finies sont non vides, mais qu'on sait aussi qu'une (au moins) de ces intersection finie est de cardinal fini alors l'intersection globale est non vide.
Donc les contres exemples sont tels que toutes les intersections finies sont de cardinal infini (donc en particulier tout les An sont de cardinal infini) puis pfuuuuit . . . l'intersection globale est vide.
Autre exemple : An = l'ensemble des entiers naturels multiple de n.
On peut aussi noter que si non seulement les intersections finies sont non vides, mais qu'on sait aussi qu'une (au moins) de ces intersection finie est de cardinal fini alors l'intersection globale est non vide.
Donc les contres exemples sont tels que toutes les intersections finies sont de cardinal infini (donc en particulier tout les An sont de cardinal infini) puis pfuuuuit . . . l'intersection globale est vide.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intersection de familles d'ensembles
Merci à vous deux, en particulier je dois me repencher sur les explications de Ben par des exemples car je saisis à moitié, mais si je comprends bien la réponse est familièrement formulée comme suit :
Pour un nombre n donné les intersections de An pour la suite ]0,1/k] est non-vide mais l'intersection de la famille des ensemble sur cette suite d'intervalles à l'infini est vide dès lors l'assertion est fausse par ce contre-exemple.
Pour un nombre n donné les intersections de An pour la suite ]0,1/k] est non-vide mais l'intersection de la famille des ensemble sur cette suite d'intervalles à l'infini est vide dès lors l'assertion est fausse par ce contre-exemple.
Re: Intersection de familles d'ensembles
Bonjour, j'avais pensé à cet exemple :

On a l'hypothèse mais pas la conclusion car quelque soit le réel x, on peut trouver > x donc x n'est pas élément de
> x donc x n'est pas élément de  donc n'est pas dans l'intersection de la famille et cette intersection est vide.
donc n'est pas dans l'intersection de la famille et cette intersection est vide.
On a l'hypothèse mais pas la conclusion car quelque soit le réel x, on peut trouver
Re: Intersection de familles d'ensembles
Bonjour à tous
J'ai un imprévu , je ne peux pas suivre l'échange davantage, j'espère qu'un autre membre sera plus disponible
@mythostyle :
en bref (à rédiger mieux, à détailler)
l'intersection des Ak pour k de 1 à n est An lui même , donc cette intersection est non vide.
il n'existe aucun réel qui appartienne à tous les Ak (à détailler) , donc l'intersection des Ak pour k de 1 à +infini est vide
Nous avons donc un contre exemple
J'ai un imprévu , je ne peux pas suivre l'échange davantage, j'espère qu'un autre membre sera plus disponible
@mythostyle :
en bref (à rédiger mieux, à détailler)
l'intersection des Ak pour k de 1 à n est An lui même , donc cette intersection est non vide.
il n'existe aucun réel qui appartienne à tous les Ak (à détailler) , donc l'intersection des Ak pour k de 1 à +infini est vide
Nous avons donc un contre exemple
Re: Intersection de familles d'ensembles
Rdvn a écrit:Bonjour à tous
J'ai un imprévu , je ne peux pas suivre l'échange davantage, j'espère qu'un autre membre sera plus disponible
@mythostyle :
en bref (à rédiger mieux, à détailler)
l'intersection des Ak pour k de 1 à n est An lui même , donc cette intersection est non vide.
il n'existe aucun réel qui appartienne à tous les Ak (à détailler) , donc l'intersection des Ak pour k de 1 à +infini est vide
Nous avons donc un contre exemple
Merci à toi !
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
