Q inter ]0,1[ ouvert ?

[744]

Alors voilà. Je cherchais un ensemble ouvert dense dans [0,1] tel que sa mesure soit inférieure à n'importe quel epsilon arbitrairement petit.
J'ai pensé à Q inter ]0,1[ , mais je suis prise d'un doute... Est-ce bien un ensemble ouvert ?
Il me semble que oui, puisqu'en chaque point de cet ensemble, on peut trouver des points infiniment proches de celui-ci, et donc une boule ouverte centrée en ce point qui soit non vide.. Mais je ne suis pas très sûre de moi. Est-ce que quelqu'un peut me le confirmer ?

[Nightmare]

Salut,

pour être un ouvert, il faut qu'en chaque point on puisse trouver une boule qui est entièrement contenue dans l'ouvert.

[Doraki]

Alors voilà. Je cherchais un ensemble ouvert dense dans [0,1] tel que sa mesure soit inférieure à n'importe quel epsilon arbitrairement petit.

c'est pas clair. Tu cherches un ensemble X tel que pour tout e>0, µ(X) 0 tu cherches un ensemble X(e) tel que µ(X(e)) < e ?

J'ai pensé à Q inter ]0,1[ , mais je suis prise d'un doute... Est-ce bien un ensemble ouvert ?
Il me semble que oui, puisqu'en chaque point de cet ensemble, on peut trouver des points infiniment proches de celui-ci, et donc une boule ouverte centrée en ce point qui soit non vide.. Mais je ne suis pas très sûre de moi. Est-ce que quelqu'un peut me le confirmer ?

Non, être ouvert ça veut dire que pour chaque point x de X, X doit contenir entièrement une boule centrée en ce point x. Quand tu parles d'une boule non vide on comprend pas ce que tu dis. Une boule ouverte n'est jamais vide par définition. Toute boule centrée en x contient x. Si tu voulais dire que pour toute boule centrée en x, l'intersection de la boule avec X est non vide (puisqu'elle contient x, déjà), ce que tu as décrit c'est que X est dense dans lui-même (et c'est vrai pour n'importe quel ensemble).

[Arkhnor]

Bonsoir,

u cherches un ensemble X tel que pour tout e>0, µ(X) 0 tu cherches un ensemble X(e) tel que µ(X(e)) < e ?

C'est très certainement la seconde proposition. (la première proposition n'admet aucune solution, un ouvert étant nécessairement de mesure non nulle)

On prend une énumération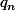 des rationnels dans [0,1], et on considère l'union des où est un intervalle ouvert contenant 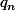et de diamètre convenablement choisi.

[barbu23]

Bonsoir, :happy3:
- Si tu travailles dans alors :
n'est pas voisinage de chacun de ses points, donc, n'est pas un ouvert de .
En effet : : ( car : contient des irrationnels )
Donc, forcement : n'est pas un ouvert de .
- Si, tu travailles dans , alors : est un ouvert de , car est un élément de la topologie trace de qui se met sous la forme avec est la topologie des ouverts de . :happy3:

[girdav]

En fait pour un fixé on peut choisir cet ouvert de façon à ce que la mesure de celui-ci soit exactement .

[Judoboy]

Trouver un ensemble de mesure nulle ça va être difficile.

Sinon essaye de construire un ensemble ouvert de mesure <= epsilon et qui contient Q inter [0;1] (indice : Q est dénombrable).