Intégration (Residus)

[LENOOBDESMATHS]

Bonjour,

J'aimerais que vous m'aidiez à résoudre l'intégrale de cette fonction :



à l'aide du théorème des résidus . Merci à vous de me donner des pistes.
La fonction est paire donc les bornes ne posent pas problème :



Et les pôles doubles sont de la forme:



Seuls et sont dans le demi_cercle qui nous intéresse.

Merci d'avance.

[Yezu]

Salut,

Utilises le lemme de Jordan avec un demi-cercle de rayon infini. Pour les calculs de résidus, étant donné que ce ne sont pas des pôles simples; il y a une formule qui donne le résidu pour un pôle d'ordre n avec des dérivées successives mais je ne pense qu'elle soit prouvée par tous les profs, car on privilégie souvent les D.L. Dans ce cas les D.L sont un peu long mais ils se font bien !
N'hésites pas à mentionner si tu cales quelque part (:

[LENOOBDESMATHS]

Salut,

Utilises le lemme de Jordan avec un demi-cercle de rayon infini. Pour les calculs de résidus, étant donné que ce ne sont pas des pôles simples; il y a une formule qui donne le résidu pour un pôle d'ordre n avec des dérivées successives mais je ne pense qu'elle soit prouvée par tous les profs, car on privilégie souvent les D.L. Dans ce cas les D.L sont un peu long mais ils se font bien !
N'hésites pas à mentionner si tu cales quelque part (:

Bonjour,

J'ai, en effet, prouvé grâce au lemme de Jordan que l'intégrale sur le demi-cercle est nulle en passant par

Cependant à l'aide de la formule de Cauchy dont vous parlez, j'obtiens :


De même :

Je pense que l'utilisation de cette formule nécessite une décomposition en éléments simples (fastideuse).
N'y a-t-il pas une autre solution plus subtile que je n'ai pas vue ? Décomposition en Série de Laurent ? En Série Entière ?

Merci d'avance pour votre aide.

[Yezu]

C'est un peu chiant je présume d'évaluer ces dérivés, si tu veux y aller à coup de D.L;
tu peux toujours poser où est un des pôles qui nous intéresse et les D.L se font franchement bien, moi perso les formules des résidus pour les pôles d'ordre je ne les utilise jamais car elles sont pénibles, un peu de manipulation avec des D.L donne les réponses en quelques lignes. Pour les produit de plusieurs D.L, ça sert à rien d'aller loin dans les puissances.
En général tu auras un terme en où qui va apparaître trivialement, donc tu n'as qu'à ramasser les plus petites puissances des produit de D.L qui te donnent un terme en .

[LENOOBDESMATHS]

C'est un peu chiant je présume d'évaluer ces dérivés, si tu veux y aller à coup de D.L;
tu peux toujours poser où est un des pôles qui nous intéresse et les D.L se font franchement bien, moi perso les formules des résidus pour les pôles d'ordre je ne les utilise jamais car elles sont pénibles, un peu de manipulation avec des D.L donne les réponses en quelques lignes. Pour les produit de plusieurs D.L, ça sert à rien d'aller loin dans les puissances.
En général tu auras un terme en où qui va apparaître trivialement, donc tu n'as qu'à ramasser les plus petites puissances des produit de D.L qui te donnent un terme en .

Je n'ai aucune idée de comment partir avec les D.L. Pourriez-vous m'en dire plus?

[Yezu]

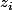
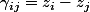
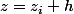
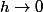
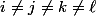
Je note un des pôles qui nous intéresse. En posant , ainsi que avec , nous avons ( les indices des pôles):
. On peut sortir les termes qui dépendent pas de pour avoir :
.
Étant donné que les D.L se font en 0, tu peux utiliser :
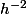
. Pour le produit des D.L, tu pourras te limiter aux termes en étant donné qu'il y a un terme en devant. La notation ne doit pas te faire peur, j'avais la flemme de calculer au long les pôles, les différences, etc. elle te permet d'avoir une expression générale pour le résidu en n'importe quel pôle.

EDIT : pour vérifier ta réponse, tu peux toujours utiliser un truc de calcul symbolique (wolfram par ex.) pour évaluer les résidus avec les dérivées.

[LENOOBDESMATHS]

Très bien, j'ai compris d'où viennent les équations.
Il me suffit de faire le D.L de et de c'est bien ça ?

Oui en effet je connais déjà le résultat que je dois obtenir.... c'est.... frustrant....

[Yezu]

Oui c'est pas mal ça, oublie pas de faire le produit des 4 par contre (:
C'est normal, calculer des résidus de pôles d'ordre >1, c'est toujours frustrant ahah