Si je comprend bien, en fait ton intégrale, ça serait
}{x-n\frac{10\pi}{19}} dx)
avec
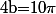
ou éventuellement
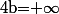
et

entier.
Dans ce cas, c'est effectivement complètement différent du cas général dont tu parle dans ton premier post : tout se "goupille bien", mais je ne pense pas que ça soit suffisant pour exprimer la valeur du truc sans utiliser la fonction sinus intégral.
Via le changement de variable

on a
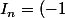^n\int_{-n\pi}^{b'}\frac{sin(y)}{y} dy=(-1)^n\int_{0}^{n\pi}\frac{sin(y)}{y} dy+(-1)^n\int_{0}^{b'}\frac{sin(y)}{y} dy)
(via la parité de la fonction)
avec
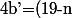\pi)
ou éventuellement
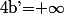
Dans le cas où b'=+oo, on connait la valeur de la deuxième intégrale, mais pour la première, à part dire que ça vaut
)
, (sinus intégral) je sais pas si on peut dire grand chose.
Bon, après, au niveau "pratique", tu peut trouver a pas mal d'endroit des tables et/ou des algorithmes permettant da calculer le
sinus intégral ...
