Intégrale d'une fonction périodique.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kiome
- Messages: 5
- Enregistré le: 10 Aoû 2009, 17:10
-
 par kiome » 10 Aoû 2009, 17:18
par kiome » 10 Aoû 2009, 17:18
Bonjour,
J'ai un problème en mathématiques du signal, mais dans mon cas ça relève davantage des mathématiques générales.
En fait j'ai une fonction périodique 2;) qui vaut soit r1, soit r2 (deux réels non nulles) et je dois trouver le résultat du calcul suivant :
(1/2;))x int(f(x)) qui vaut (r1+r2)/2 (où int signifie intégrale)
Cependant je n'arrive pas à le trouver mathématiquement. En faisant un schéma ça pose pas de souci, mais comment le prouver par le calcul ?
Merci.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 10 Aoû 2009, 17:20
par xyz1975 » 10 Aoû 2009, 17:20
Donnes au moins la fonction et les deux réels.
-
kiome
- Messages: 5
- Enregistré le: 10 Aoû 2009, 17:10
-
 par kiome » 10 Aoû 2009, 17:33
par kiome » 10 Aoû 2009, 17:33
La fonction est périodique 2;) et vaut :
r1 si t appartient à l'intervalle [-;),0[ et
r2 si t appartient à l'intervalle [0,;)[.
r1 et r2 sont des réels quelconques, il peuvent valoir 1, 5, -2,3 etc.
Merci.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 10 Aoû 2009, 17:39
par xyz1975 » 10 Aoû 2009, 17:39
Dans ta question tu n'as pas donné les bornes de l'intégrale de f.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 10 Aoû 2009, 17:48
par xyz1975 » 10 Aoû 2009, 17:48
Par exemple :
dx=\bigint_{-\pi}^{0}r_1dx+\bigint_{0}^{\pi}r_2dx)
Le reste c'est facile à faire.
-
kiome
- Messages: 5
- Enregistré le: 10 Aoû 2009, 17:10
-
 par kiome » 10 Aoû 2009, 17:49
par kiome » 10 Aoû 2009, 17:49
L'intégrale est sur une période, donc soit de -;) à 0 ou de 0 à ;).
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 10 Aoû 2009, 17:54
par xyz1975 » 10 Aoû 2009, 17:54
Sur une période cela veut dire par exemple sur
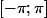
puisqu'elle est

-périodique.
regardes le message 5 il te donne tout.
-
kiome
- Messages: 5
- Enregistré le: 10 Aoû 2009, 17:10
-
 par kiome » 11 Aoû 2009, 09:33
par kiome » 11 Aoû 2009, 09:33
Justement c'est ça que j'ai du mal à me souvenir ou à refaire...
Quelle le résultat de l'intégrale de r1 sur 0, pi ?
r1 étant une constante, on le sort de l'intégrale et on obtient intégrale de 1 = 1 ?
Merci. :)
-
mathelot
 par mathelot » 11 Aoû 2009, 09:40
par mathelot » 11 Aoû 2009, 09:40
les intégrales sont des aires (signées) de rectangles :zen:
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 11 Aoû 2009, 11:50
par xyz1975 » 11 Aoû 2009, 11:50
mathelot a écrit:les intégrales sont des aires (signées) de rectangles :zen:
Je ne suis pas du tout d'accord avec toi :
L'intégrale n'est ni aire ni volume mais un volume et une aire est bien une intégrale.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
