Salut,
Déjà, je te rassure tout de suite, c'est pas toi "qui te trompe" en ne sachant pas ce que signifie "la région entre ...", mais c'est le type qui a posé l'énoncé qui est un âne bâté : Autant sur R où il y a une relation d'ordre, la notion de "réel compris entre deux réels fixés" est parfaitement cohérente, autant dans R^2 ou R^3 où il n'y a pas de relation d'ordre, ben ça veut rien dire du tout.
Si un mec te dit de considérer sur la terre "la région comprise entre l'équateur et le méridien de Greenwitch ", tu pense que ça a du sens ?Bon, après, en général, dans ce genre d'exo., le domaine en question il est borné donc parmi les 4 domaines "délimités" par tes équations (selon le sens dans lequel on met les inégalités), il y a a deux que
SEMBLENT exclus (mais c'est tout sauf une certitude au sens mathématique du mot "certitude") mais concernant les deux dernier, je vois pas quel argument (forcément non mathématique) permettrait de trancher.
Bref, y'a qu'a dire que le domaine en question, c'est bien celui qui est au dessus du cône et en dessous de la sphère (ou les expressions "au dessus" et "en dessous" sont, comme à peu prés toujours dans R^3, relative à l'ordre sur l'axe des z).
Mais il faut effectivement être parfaitement conscient que c'est du "
au pif complet"...
Sinon, concernant la suite, je t'inciterais plus que fortement à commencer par écrire ça :
Vu que l'énoncé est complètement ambiguë, je considère que la région dont il parle est l'ensemble des (x,y,z) tels que ) AVEC DES INEGALITES
AVEC DES INEGALITES et pas des égalités.
Et concernant la suite, tu ne manipule (quasiment)
que des inégalités et pas des égalités.
Par exemple, si tu passe en coordonnées cylindriques,
commence par écrire en toute lettres que tu pose
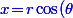\ ;\ y\!=\!r\sin(\theta)\ ;\ z\!=\!z)
avec
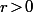
et
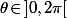
(ou un autre intervalle de largeur

)
Puis que
\ \Leftrightarrow\ r^2\!-\!1\!\leq\!z\leq\!\sqrt{1\!-\!r^2})
Ce qui te donne le domaine dans lequel va varier

pour

connu.
Et pour trouver dans quel domaine varie

tu résout évidement
l'inéquation 
.
En bref et en résumé, tu arrivera à faire des trucs dans ce type d'exo. le jour ou tu comprendra que tes domaines, ils sont définis par des inéquation et pas par des équations...
