Intégrale de Gauss
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 17 Sep 2012, 21:22
par Supernova » 17 Sep 2012, 21:22
Svp, comment calculer l'intégrale de Gauss par une >>>> IPP <<<<
???
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 17 Sep 2012, 21:32
par Supernova » 17 Sep 2012, 21:32
Merci, mais nous avons par encore étudié les fcts à plusieurs variables :/
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 17 Sep 2012, 21:35
par Kikoo <3 Bieber » 17 Sep 2012, 21:35
Hmmm... Je sais pas. Perso je vois pas d'autre façon de la calculer cette fameuse intégrale.
Et pas moyen de trouver une primitive "exprimable avec des fonctions usuelles, tu vois ce que je veux dire ?".
Une primitive de ce machin est la fonction erf (error function).
Heu t'es en MP et t'as pas vu les intégrales multiples ??
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 17 Sep 2012, 21:39
par Supernova » 17 Sep 2012, 21:39
Si, on les utilise en physique et en SI mais pas en maths, d'ailleurs les fct à plusieurs variable ont été retirées du programme de MPSI..
Mon problème c que mon prof nous a donné comme indication d'utiliser une IPP
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 17 Sep 2012, 21:40
par Kikoo <3 Bieber » 17 Sep 2012, 21:40
Supernova a écrit:Si, on les utilise en physique et en SI mais pas en maths, d'ailleurs les fct à plusieurs variable ont été retirées du programme de MPSI..
Mon problème c que mon prof nous a donné comme indication d'utiliser une IPP
Bon ben je vais laisser ma place à des gens plus compétents alors

Bonne nuit !
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 17 Sep 2012, 21:43
par Mathusalem » 17 Sep 2012, 21:43
Supernova a écrit:Mon problème c que mon prof nous a donné comme indication d'utiliser une IPP
Ben tu peux pas
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 17 Sep 2012, 21:43
par Supernova » 17 Sep 2012, 21:43
Ne dis pas ça!
Bn8 à toi aussi
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 17 Sep 2012, 21:44
par Supernova » 17 Sep 2012, 21:44
C'est ce que je pensais, bsinn y a pas une autre méthode plus simple?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 17 Sep 2012, 21:45
par Kikoo <3 Bieber » 17 Sep 2012, 21:45
Supernova a écrit:Ne dis pas ça!
Je ne me vexe pas ne t'inquiète pas

C'est juste que je m'y connais pas assez sur ce domaine, c'est tout. Je veux pas te dire de conneries !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 17 Sep 2012, 21:52
par Kikoo <3 Bieber » 17 Sep 2012, 21:52
Supernova a écrit:C'est ce que je pensais, bsinn y a pas une autre méthode plus simple?
Non, pas d'autre méthode apparemment, si déjà qu'avec n'importe qu'elle méthode compliquée t'y arrives pas ^^
C'est comme donner une primitive à ln(x)/x
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 17 Sep 2012, 21:58
par Supernova » 17 Sep 2012, 21:58
Ok :D g compriis
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 17 Sep 2012, 22:06
par Luc » 17 Sep 2012, 22:06
Supernova a écrit:Ok

g compriis
Salut,
il y a d'autres méthodes mais le passage en coordonnées polaires est la plus simple. Il y a en a une qui utilise la méthode des résidus pour les fonctions de variable complexe. Je crois aussi une autre avec une équation différentielle.
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 17 Sep 2012, 22:13
par Billball » 17 Sep 2012, 22:13
Luc a écrit:Salut,
il y a d'autres méthodes mais le passage en coordonnées polaires est la plus simple. Il y a en a une qui utilise la méthode des résidus pour les fonctions de variable complexe. Je crois aussi une autre avec une équation différentielle.
exact pour l'équation différentielle mais fait intervenir la fourier transform me semble t-il!
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 17 Sep 2012, 22:13
par Supernova » 17 Sep 2012, 22:13
Trop compliqué; sinon on peut chercher un équivalent de cette intégrale..
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 17 Sep 2012, 22:36
par Luc » 17 Sep 2012, 22:36
Supernova a écrit:Trop compliqué; sinon on peut chercher un équivalent de cette intégrale..
c'est a dire?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 17 Sep 2012, 22:41
par Luc » 17 Sep 2012, 22:41
Billball a écrit:exact pour l'équation différentielle mais fait intervenir la fourier transform me semble t-il!
Exact : la fonction x-> exp(-x^2) a la propriété dêtre un point fixe de la transformée de Fourier dans L2 (avec les bonnes constantes)!
La transformée de Fourier est un opérateur linéaire. Il est intéressant de regarder ces vecteurs propres. On peut montrer qu'ils sont en lien direct avec les polynômes de Hermite et la fonction x-> exp(-x^2).
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 27 Sep 2012, 21:10
par Supernova » 27 Sep 2012, 21:10
Luc a écrit:c'est a dire?
cad une effectue une IPP, ça donne:
e^-x^2/2x - l'intégrale(x...oo) e^t^2/2 t^2 dt
et on a e^-t^2/t^2 = o(e^-t^2)
donc l'intégrale(0...oo) e^-t^2 dt = e^-x^2/2x + o(l'intégrale(x..oo) e^-t^2/t^2 = o(e^-t^2))
d'où l'intégrale de Gauss ~ e^-x^2/2x
PS: Dsl pour la mauvaise écriture
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 27 Sep 2012, 21:20
par Luc » 27 Sep 2012, 21:20
J'essaye de réécrire ce que tu as écrit, dis moi si c'est bon.
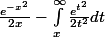
et on a
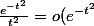)
donc l'intégrale
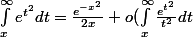= o(e^{-x^2}))
d'où l'intégrale de Gauss
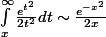
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 27 Sep 2012, 21:26
par Supernova » 27 Sep 2012, 21:26
Luc a écrit:J'essaye de réécrire ce que tu as écrit, dis moi si c'est bon.
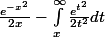
et on a
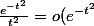)
donc l'intégrale
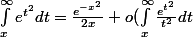= o(e^{-x^2}))
d'où l'intégrale de Gauss
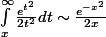
Yep! c parfait

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
