Intégrale de Gauss

[upium666]

Bonjour à tous et à toutes
Je ne suis qu'en 1ère S et je ne maîtrise donc pas vraiment le sujet mais je vous prie de m'aider, sans besoin de me simplifier les choses

On se propose de calculer :



Sans démonstration (je ne le peux pas, j'ai cherché un peu sur internet :triste: ) je suis arrivé à ce résultat :



ou de manière plus simple :



Comment puis-je continuer pour arriver au calcul voulu ? (en valeurs exactes ! C'est à peu près 0.7468241... je pense mais je veux la valeur exacte)

Merci !

[leon1789]

voir ici http://www.maths-forum.com/integrale-gauss-140432.php

[leon1789]

(attention, c'est (-1)^k )

Je pense que tu ne pourras pas faire mieux que cette somme, car avec les fonctions usuelles, on ne peut pas exprimer de manière exacte l'intégrale que tu proposes.

D'ailleurs, la fonction est pris comme référence (on lui donne le nom de "fonction d'erreur") pour exprimer les intégrales de Gauss.http://fr.wikipedia.org/wiki/Fonction_d'erreur

[upium666]

(attention, c'est (-1)^k )

Je pense que tu ne pourras pas faire mieux que cette somme, car avec les fonctions usuelles, on ne peut pas exprimer de manière exacte l'intégrale que tu proposes.

D'ailleurs, la fonction est pris comme référence (on lui donne le nom de "fonction d'erreur") pour exprimer les intégrales de Gauss.http://fr.wikipedia.org/wiki/Fonction_d'erreur

Je sais, et c'est pour ça que j'ai bloqué :s ...
Car elle est pris comme référence !

L'intégrale que je cherche se trouve avoir la valeur

Ce que j'ai pensé à faire, c'est essayer d'obtenir une valeur exacte de erf(1) puisqu'elle est exprimable sous forme de fraction continue ...

?

[leon1789]

Ce que j'ai pensé à faire, c'est essayer d'obtenir une valeur exacte de erf(1) puisqu'elle est exprimable sous forme de fraction continue ...

C'est peut-être possible de décrire une fraction continue (avec évidemment un nombre de termes infini) égale à erf(1), je ne sais pas, je n'y connais pas grand chose (mais ça m'a l'air complètement chaotique vu les premiers termes).

Mais ce qui m'étonne encore, c'est
-1- l'expression "obtenir une valeur exacte" (ça veut dire quoi pour toi ?)
-2- la justification "puisque" ... (je ne vois pas ce que tu attends de la fraction continue)

[upium666]

-1- l'expression "obtenir une valeur exacte" (ça veut dire quoi pour toi ?)

Les convergences des séries ne mènent-elles pas à des irrationnels par exemple ?
Notre intégrale dépend d'une valeur exacte, "connue" ( ) : le résultat devrait en dépendre et donc s'exprimer par exemple en fonction de ?

-2- la justification "puisque" ... (je ne vois pas ce que tu attends de la fraction continue)

Vous connaissez sûrement la célèbre expression (du nombre d'or) :

Avec ou sans l'utilisation des suites, on aboutit à la résolution de l'équation dont une des deux solutions correspond à la valeur recherchée, qui donne EXACTEMENT
C'est ça ce que j'attends d'une fraction continue ...

Pourrait-on faire de même ? ...

[leon1789]

ah, en guise de réponse, une petite tartine s'impose... :lol3:

Les convergences des séries ne mènent-elles pas à des irrationnels par exemple ?

si bien sûr, et justement tu as exhibé une série dont la valeur est égale à l'intégrale. D'ailleurs, il existe (une infinité) d'autre séries qui ont la même valeur...
Mais est-ce cela te satisfait ? j'ai l'impression que non, puisque tu continues à chercher une valeur "exacte".

Notre intégrale dépend d'une valeur exacte, "connue" ( ) : le résultat devrait en dépendre et donc s'exprimer par exemple en fonction de ?

ah... ce que tu dis amène plein de questions ! valeur exacte, dépendre de, s'exprimer avec...

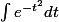
L'intégrale est un réel, que je vais noter I.
Est-ce que ton intégrale I dépend de "e" ou de "pi" ?
Est-ce que "e" dépend de "pi" ? Et réciproquement ?
Est-ce qu'un réel dépend d'un autre réel ?... cela n'a pas vraiment de sens.

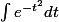
e apparaît dans l'expression qui vaut I, ok.
pi apparaît dans l'expression qui vaut I aussi.
ni e, ni pi, ni , ni ln(3), n'apparaissent dans qui vaut pourtant I !

Bref, ne pas confondre une expression (une formule) et la valeur de l'expression (un réel).

De plus, que signifie "exact" ? C'est un mot que beaucoup de gens utilisent, mais qui n'est jamais vraiment bien défini pour eux. Du coup, cela crée des quiproquos...
Tu dis que >. Pour moi, "e" est un symbole qui désigne un réel précis (que je peux présenté comme étant l'image de 1 par la fonction expentionelle, ou sous d'autres formes encore), tout comme pi désigne un réel précis (le ratio entre la circonférence d'un cercle et la longueur d'un diamètre, par exemple), ...tout comme I désigne un réel précis (présenté par ton intégrale, ou les séries que tu as données, ou autrement encore)

Bref, ne pas confondre un symbole (une notation) et un réel (qui a une valeur précise, mais plus ou moins bien connue par nous, "pauvres humains").

Pour moi, l'adjectif "exact" est à mettre en opposition avec "approché" :
2.718 est une valeur approché de e,
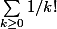
et donne la valeur exacte de "e".


Pour l'instant, pour moi, ce que tu dis est flou. Mais c'est normal, tu apprends, tu découvres, tu "intuites"...

Vous connaissez sûrement la célèbre expression (du nombre d'or) :

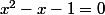
Avec ou sans l'utilisation des suites, on aboutit à la résolution de l'équation dont une des deux solutions correspond à la valeur recherchée, qui donne EXACTEMENT
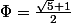
C'est ça ce que j'attends d'une fraction continue ...

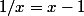
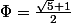
En l'occurrence, sur cet exemple de , je crois que tu as mis la charrette avant les boeufs, car on connait d'abord comme solution de donc , puis on a calculé le développent continu de .

Mais ok, je comprends ce que tu veux dire.

Pourrait-on faire de même ? ...

On pourrait peut-être trouver une description complète du développement en fraction continue de ton réel I (moi, je ne connais pas) : ce sera difficile si personne ne l'a déjà trouvé... Ce serait un petit miracle.

Ensuite, on pourrait peut-être trouver une équation polynomiale (comme tu as présentée, mais de degré beaucoup plus grand !) dont I serait une solution : cela signifierait que le réel I est algébrique, ce qui est très peu probable pour un réel... Ce serait un gros miracle.

Et enfin, il faudrait résoudre de manière exacte (et non approchée) l'équation pour déterminer une nouvelle expression du réel I. Là, je n'y crois pas du tout, car, comme je te le disais, il n'y a pas d'expression de I qui n'utilise que des opérations et fonctions "usuelles".


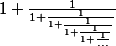
Et pour conclure mon message, l'expression de donnée par n'est pas plus exacte que le développent . A la rigueur, c'est juste une expression plus simple d'emploi que le développement continu.
Est-ce que tu cherches une expression de I plus facile d'emploi que l'intégrale ou que la série que tu as déjà fournies ?

[leon1789]

Ton problème n'est-il pas de trouver une expression de I plus facile d'emploi que l'intégrale ou que la série que tu as déjà fournies ?

[upium666]

Ton problème n'est-il pas de trouver une expression de I plus facile d'emploi que l'intégrale ou que la série que tu as déjà fournies ?

Je chercherais plutôt la limite suivante qui conduit à la valeur "approchée" (vous n'aimez pas ce terme :p ) 0.74 :



Mon problème maintenant, sachant que
est de trouver erf(1) tout comme on a pu trouver la valeur de !
En essayant de trouver une valeur que POURRAIT (conditionnel !) nous procurer la formule en fraction continue ...

:hum:

[leon1789]

:id: joli ! Je ne connaissais pas cette formule. Cela dit, elle converge lentement...

[leon1789]

Mon problème maintenant, sachant que
est de trouver erf(1) tout comme on a pu trouver la valeur de !

:id: joli ! Je ne connaissais pas cette formule. Cela dit, elle converge lentement, mais peu importe !
Cela fait donc une troisième manière de présenter I.

Pour le reste, je pense que tu "rêves un peu" comme on dit platement :lol3:

[upium666]

:id: joli ! Je ne connaissais pas cette formule. Cela dit, elle converge lentement, mais peu importe !
Cela fait donc une troisième manière de présenter I.

Pour le reste, je pense que tu "rêves un peu" comme on dit platement :lol3:

Pour ce qui est de rêver, c'est sûr ! :ptdr:
Mais bon, je n'y perds rien (ce n'est même pas au programme de lycée)

Sachant que je compte essayer une dernière fois, que me conseilleriez-vous de faire ?
Autrement dit : Puis-je exprimer I en fonction de constantes usuelles ( , , etc...), de nombres réels, etc... ?

[leon1789]

Pour ce qui est de rêver, c'est sûr ! :ptdr:
Mais bon, je n'y perds rien

Non seulement tu n'y perds rien, mais tu y gagnes du plaisir, c'est important.

Sachant que je compte essayer une dernière fois, que me conseilleriez-vous de faire ?
Autrement dit : Puis-je exprimer I en fonction de constantes usuelles ( , , etc...), de nombres réels, etc... ?

Il est certain qu'il n'est pas possible d'exprimer I à l'aide des constantes usuelles et des opérations usuelles.

Pour les trois formules que tu as présentées, les opérations ne sont pas qualifiées d'usuelles : intégration, série, fraction continue. Il y a surement d'autres formules qui donnent I, je n'en connais pas (because manque de culture sur le sujet).

[upium666]

Je vous remercie ! :we:

:lol3:

(Si j'y arrive je vous en ferais bien part :we: !)
(Va rêver :dodo: :ptdr: )

:lol3:

[upium666]

Ce à quoi je veux arriver en fait, et c'est là où c'est "impossible", c'est d'arriver à trouver UNE VALEUR à ce I que vous jugez inexprimable autrement.

Je prends le simple exemple de qu'on jugeait inexprimable jusqu'à ce que ce grec dont m'échappe le nom démontre que c'est en réalité EGAL A
C'est à ça que je veux arriver !

Vous comprenez mieux ? :ptdr:

[leon1789]

Ce à quoi je veux arriver en fait, et c'est là où c'est "impossible", c'est d'arriver à trouver UNE VALEUR à ce I que vous jugez inexprimable autrement.

Je prends le simple exemple de qu'on jugeait inexprimable jusqu'à ce que ce grec dont m'échappe le nom démontre que c'est en réalité EGAL A
C'est à ça que je veux arriver !

Vous comprenez mieux ? :ptdr:

oui, je comprends très bien. Mais bon...

Regarde ici une autre discussion où on en dit un peu plus.
Ou ce document...

Tiens aussi http://mathworld.wolfram.com/Erf.html : il y a beaucoup de choses qui vont te plaire !