Bonjour
Soit D = [0;1] x [0;1], calculer l'intégrale double de abs(x-y) sur D
Il faut donc distinguer le cas où x-y>0 et x-y<0 mais je ne sais pas comment définir les bornes propres à chaque cas ?
Cordialement
Intégrale double
7 messages
- Page 1 sur 1
Re: Intégrale double
Bonjour
Le domaine (un carré) est coupé en deux par la droite y=x. Soit la partie de D contenant les couples (x,y)
la partie de D contenant les couples (x,y)
vérifiant x>y. A cause de la symétrie, l'intégrale vaut 2 fois l'intégrale sur . On calcule donc l'intégrale sur
. On calcule donc l'intégrale sur  On a
On a 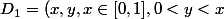 (faire un dessin).
(faire un dessin).
On a donc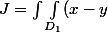 dx dy=\int_{x=0}^1 (\int_{y=0}^x (x-y) dy) dx =....)
Le domaine (un carré) est coupé en deux par la droite y=x. Soit
vérifiant x>y. A cause de la symétrie, l'intégrale vaut 2 fois l'intégrale sur
On a donc
Re: Intégrale double
Merci
Pour D1, j'obtiens (1/2)*(x-x^2) donc l'intégrale de la valeur absolue de x-y sur D vaut x-x^2
Est-ce bien cela ?
Pour D1, j'obtiens (1/2)*(x-x^2) donc l'intégrale de la valeur absolue de x-y sur D vaut x-x^2
Est-ce bien cela ?
Re: Intégrale double
Non l'intégrale est un nombre donc ne dépend pas de x .
Je continue le calcul de J:
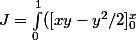 dx)
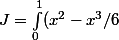 dx=7/24)
L'intégrale de départ est donc 2J.
Je continue le calcul de J:
L'intégrale de départ est donc 2J.
Re: Intégrale double
On commence par le calcul de l'intégrale à l'intérieur (donc on intègre par rapport à y.
Donc la primitive est donc
donc  (oui c'est ça)
(oui c'est ça)
Donc la primitive est
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
