Voici une double intégrale.
Avec
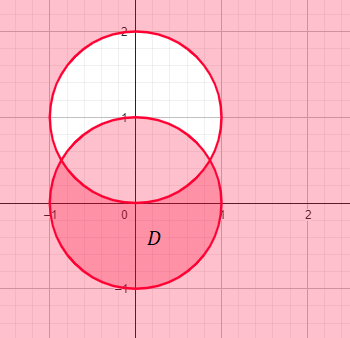
Pour le moment, je souhaite représenter le domaine D.
Est-ce que cela ressemble au dessin ci-dessous, le demi-cercle est D.
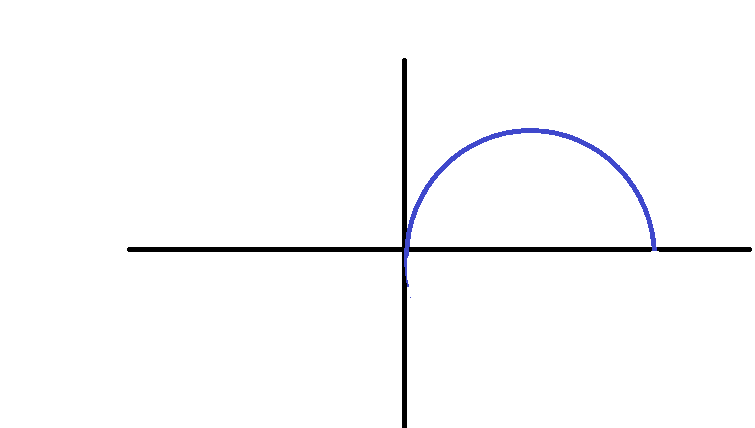
A bientôt


Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :