Primitive d'une fonction sqrt
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 08 Nov 2008, 22:07
par fourize » 08 Nov 2008, 22:07
bonjour !
de l'intégration par partie aux changement de variables;
rien n'aboutit au primitive de la fonction
)
ou sqrt => racine carré
donc j'aimerai bien un coup de pouce!
merci !
modification: écriture correcte de la fonction
* In God we trust, for all others bring data *
-
rugby09
- Membre Rationnel
- Messages: 992
- Enregistré le: 04 Déc 2007, 17:25
-
 par rugby09 » 08 Nov 2008, 22:44
par rugby09 » 08 Nov 2008, 22:44
fourize a écrit:de l'intégration par partie aux changement de variables;
rien n'aboutit au primitive de la fonction x²/sqrt(1-x²)
ou sqrt => racine carré
!
sqrt? c'est pour le
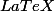
non?


-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 08 Nov 2008, 23:27
par fourize » 08 Nov 2008, 23:27
salut !!
au fait! rugby09 j'aimerai savoir comment tu fais pour écrire les fontions aussi bien. si tu t'y connais en informatique . dis moi comment trouver la bibliotheque (ou balises) mathematique de ce forum MERCI D'AVANCE.
pour le changement de variable ça a l'air de marcher; mais on se retrouve à calculer la primive de arcsin(x)???? que je sais pas comment? "angelique_64 :hein: "
un peu plus d'explication ou un autre piste car celui la, ne marche pas!
fourize
* In God we trust, for all others bring data *
-
rugby09
- Membre Rationnel
- Messages: 992
- Enregistré le: 04 Déc 2007, 17:25
-
 par rugby09 » 08 Nov 2008, 23:32
par rugby09 » 08 Nov 2008, 23:32
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 08 Nov 2008, 23:39
par Purrace » 08 Nov 2008, 23:39
Pose sin(t)=x !
-
j_e
- Membre Naturel
- Messages: 70
- Enregistré le: 02 Nov 2008, 11:08
-
 par j_e » 08 Nov 2008, 23:59
par j_e » 08 Nov 2008, 23:59
\int\frac{x^2}{\sqrt{1-x^2}}dx
Donne avec les balises "TEX" :

\int : le symbole de l'intégrale
\frac{...}{...} : pour faire des fractions (première accolade : num ; deuxième : dénom)
\sqrt{...} : pour faire des racines carrées
C'est pas très difficile

Par contre, le calcul de l'intégrale l'est sans doute un peu plus

Purrace propose le changement de variable
 = x)
, on a alors
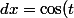\cdot dt)
, et donc :

La formule fondamentale de la trigonométrie devrait t'aider à avancer ...
Bon courage !

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 09 Nov 2008, 00:06
par fourize » 09 Nov 2008, 00:06
Purrace a écrit:Pose sin(t)=x !
salut
avec ça on trouve le primitive est (-1/4)sin2t + (1/2)t
normalement on devait changer te x=arcsint
ce qui pose de enorme probleme avec le sin2t???
merci de votre aide mais je suis toujours pas debloqué
* In God we trust, for all others bring data *
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 09 Nov 2008, 01:34
par Purrace » 09 Nov 2008, 01:34
Sin(2t)=2costsint

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 09 Nov 2008, 15:32
par fourize » 09 Nov 2008, 15:32
Angélique_64 a écrit:u(x) =x et v ' (x) = x /sqrt( 1-x²)
donc u' (x) =1 et on choisit v (x) = -sqrt (1-x²)
L'intégrale I devient: [ x*sqrt (1 -x²) ] + intégrale (sqrt(1-x²))
Il reste à remarquer que sqrt(1-x²) = (1-x²)/ sqrt(1-x²) = 1/sqrt(1-x²) - x²/sqrt(1-x²)
on a une équation qui permet de trouver l'intégrale initiale!
Voilà, voilà
PS Il faut se méfier des changements de variables quand les bornes sont inconnues car le changement doit s'opérer de manière bijective
bonjour !
oui pour l'egalité initiale mais en posant F la primitive chercher;
on se trouve avec (1/2)F=(1/2)xsqrt(1-x²) +
integra(1/sqrt(1-x²))que je vois pas comment la calculer.
n'oublie pas que (1-x²)' ne fait pas 1 mais -2x qu'on ne peut pas ajouter
quand t'on veut :triste:
tu vois un peu Angelique_64?
"je suis aussi d'accord pour ta proposition sur les bornes; mais on cherche
désespérément et on vera bien les conditions qui vont avce ...
* In God we trust, for all others bring data *

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 09 Nov 2008, 19:59
par fourize » 09 Nov 2008, 19:59
Angélique_64 a écrit:la fonction x --> arcsinus x, n'aurait elle pas justement comme dérivée:
x --> 1/ sqrt(1-x²) ????
ben si justement ; mais je vois comment ça peut nous aider franchement?
fin pas grand chose quoi

* In God we trust, for all others bring data *

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 09 Nov 2008, 20:48
par fourize » 09 Nov 2008, 20:48
salut angelique_64 et tout le monde bien sur!
tout d'abord; merci pour le tuyau, ça à l'air bon
mais t'as fait plait de calcule à la louche que ca me complique.
du v'=x/sqrt(1-x²) => sqrt(1-x²) au lieu de (-1/2)sqrt(1-x²) ...
t'as zappé tout les coeffients et moi qui garde; je trouve:
3F=x*sqrt(1-x²) + arcsin(x)
par verification c est la primitive de -x(x+1)/sqrt(1-x²) et pas celle voulu !?
je juge pas; c'est juste si je fais de erreur que tu me signal ; encore une
fois MERCI je vais refaire tout pour voir si ce n'est pas mes neurones qui dérapent xD.
une autre piste sera la bienvenu car celui la est un peu penible :id:
* In God we trust, for all others bring data *
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 09 Nov 2008, 21:40
par Purrace » 09 Nov 2008, 21:40
Un changement de variable fonctionne tres tres bien , vu qu'on pose pas de condition aux bornes .

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 11 Nov 2008, 11:07
par fourize » 11 Nov 2008, 11:07
bonjour !
je tiens à remercier tout ce qui on le courage de me lire dans le but de m'aider;
et à remercier vivement ce qui mon aider en participant à cette discussion.
pour laisser le sujet bénéfique au génération futur qui aurons le même
problème; je résume ici les procedures et la solution à trouvé.
-on fait une intégration par partie (comme à dit angelique_64 avec sa remarque)
-et surtout pas de changement de variable"qui conduit en général a l'erreur".
on trouve finalement :
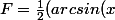 - x*sqrt(1-x^2)))
je remercie également uztop et rugby09 qui ; grâce à eux j'écrirai les formules
mathématique sans difficulté
fourize
* In God we trust, for all others bring data *
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités